Предмет: Математика,
автор: InWonderLand
Определить сходится или расходится ряды
Приложения:
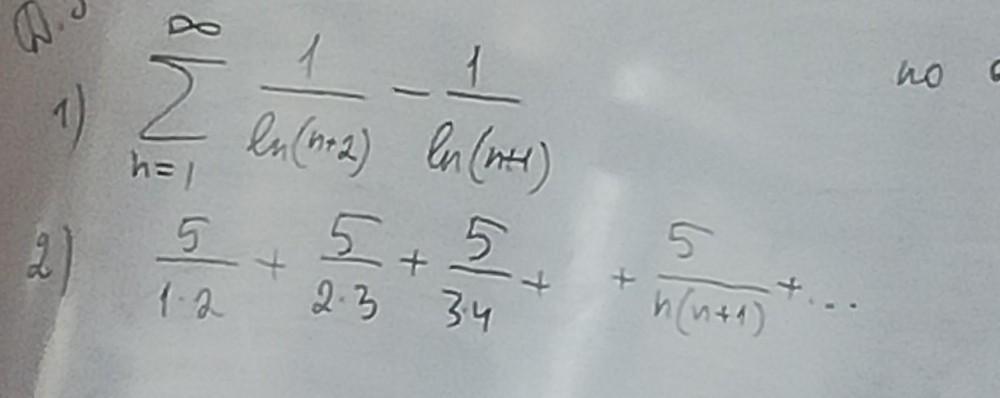
IrkaShevko:
оба сходятся
Где доказательство?
так и пишу в комментариях, чтобы не писать решение
Ответы
Автор ответа:
0
Ответ: оба ряда сходятся.
Пошаговое объяснение:
1) n-ная сумма ряда имеет вид: Sn=1/ln(3)-1/ln(2)+1/ln(4)-1/ln(3)+....+1/ln(n+2)=1/ln(n+2)-1/ln(2). Перехода к пределу при n⇒∞, находим S=lim Sn=0-1/ln(2)=-1/ln(2). Поэтому ряд сходится.
2) n-ный член ряда имеет вид an=5/[(n*(n+1)]=5/n-5/(n+1). Тогда n-ная сумма ряда Sn=5-5/2+5/2-5/3+5/3-5/4+.....+(-5/(n+1)=5-5/(n+1). Переходя к пределу, находим S=lim(n⇒∞) Sn=5-0=5 - значит, ряд сходится.
Похожие вопросы
Предмет: Английский язык,
автор: valeriazerebec
Предмет: Химия,
автор: polliffem
Предмет: Русский язык,
автор: HUMAN2483
Предмет: Литература,
автор: sfazullina
Предмет: Математика,
автор: VarVaraaaa1