Предмет: Алгебра,
автор: kkkkkkkkkkgguffy
помогите решить рациональным путем
Приложения:
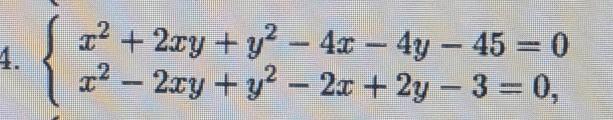
Ответы
Автор ответа:
1
1 случай:
2 случай:
3 случай:
4 случай:
Ответ: (-3; -2), (1; -4), (4; 5), (6; 3).
Похожие вопросы
Предмет: Английский язык,
автор: eninaoks72
Предмет: Химия,
автор: asuslova010
Предмет: Математика,
автор: linkotima
Предмет: Математика,
автор: Аноним
Предмет: История,
автор: semchuk1983