Предмет: Геометрия,
автор: zaitsevsergey12
вершина b параллелограмма abcd соединена с точкой m на стороне cd отрезок bm пересекает диагональ ac в точке k Площадь треугольника bck=18 а площадь треугольника cmk =12
Найти площадь паралеллограмма
dnepr1:
Не хватает данных! Положение точки К или М необходимо!
Ответы
Автор ответа:
2
У треугольников BKC и KCM общая высота, то их площади относятся как основания, т.е.
по двум углам и коэффициент подобия k = BK/KM = 3/2. Тогда отношение площадей подобных треугольников равно квадрату коэффициента подобия.
кв. ед.
кв. ед.
Тогда кв. ед.
Приложения:
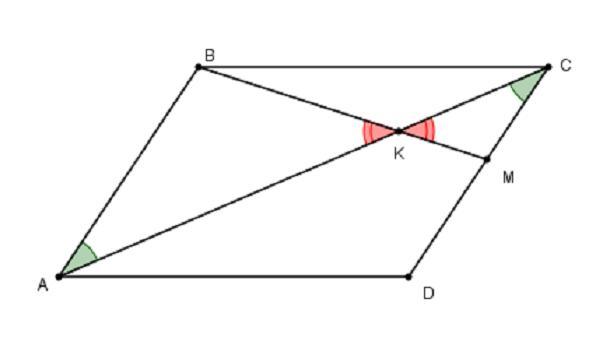
Надо исправить решение: Площадь треугольника bck=18. ВК/КМ = 3/2.
спасибо. Попрошу на исправление
Похожие вопросы
Предмет: История,
автор: mirgorod210
Предмет: Математика,
автор: nazarchucnadia
Предмет: Алгебра,
автор: Мозгокошка
Предмет: Литература,
автор: Funtik1234