Предмет: Геометрия,
автор: pula2012
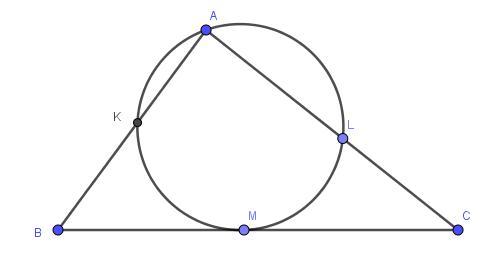
Помогите, пожалуйста, решить. Окружность, проходящая через вершину А треугольника АВС, касается стороны ВС в точке М и пересекает стороны АС и АВ соответсвенно в точках L и К, отличных от вершины А. Найдите отношение АС:АВ, если известно, что длина отрезка LC в два раза больше длины отрезка КВ, а отношение СМ:ВМ=3:2
Ответы
Автор ответа:
5
По теореме о секущей и касательной:
Из условия LC = 2KB . Рассмотрим отношение
Ответ: 9 : 8.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: UlyanaaaZaavg
Предмет: Математика,
автор: lerakolodko575
Предмет: Математика,
автор: gannalitvinova3476
Предмет: Алгебра,
автор: oksankaanufrie
Предмет: Химия,
автор: Ainurik15