Question

Дан прямоугольный треугольник ABC с прямым C углом . Пусть BK — биссектриса этого треугольника. Окружность, описанная около треугольника AKB , пересекает вторично сторону BC в точке L . Найдите CB+CL , еcли AC=4 AB=5 .

Answer 1

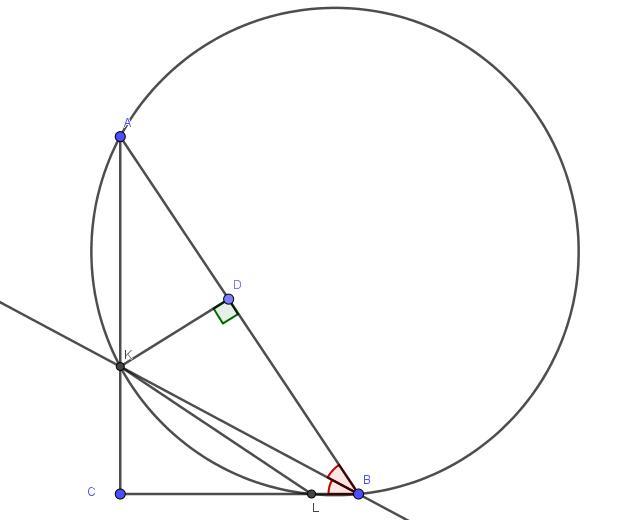
BK - биссектриса угла ABC, следовательно, ∠ABK = ∠KBC. Из точки K проведем перпендикуляр KD к стороне AB. ΔKDB = ΔCKB по гипотенузе и острому углу ⇒ BD = BC и KD = KC.

∠ABK опирается на дугу AK и ∠LBK опирается на дугу KL, то есть, хорды AK и KL опираются равные углы, поэтому AK = KL отсюда следует, что ΔKAD = ΔLCK по гипотенузе и катету ⇒ AD = CL, таким образом CB + CL = BD + AD = AB = 5

Answer 2

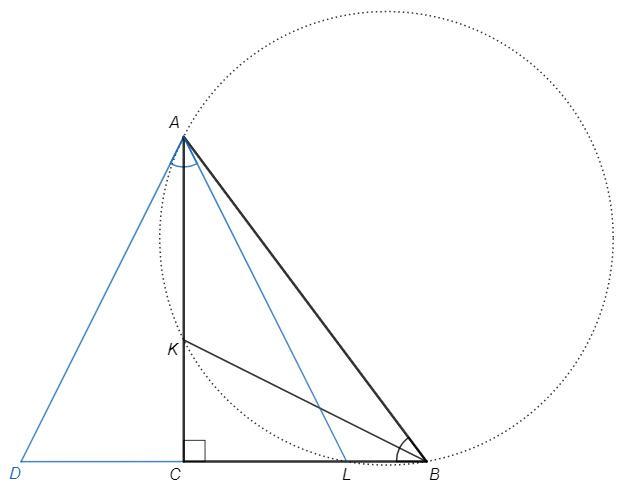
На продолжении BC отложим отрезок CD, равный СL.

В треугольнике DAL отрезок AC является высотой и медианой, следовательно и биссектрисой, треугольник равнобедренный.

DAL =2KAL =2∪KL/2 =2KBL =ABD

△DAL~△DBA (по двум углам) => △DBA - равнобедренный.

BC+CL =BC+CD =BD =BA =5