Вокруг трапеции описано круг. Найти радиус круга, если основания трапеции 20 см и 12 см, угол между боковой стороной трапеции и основой равен 30 градусов.
Ответы
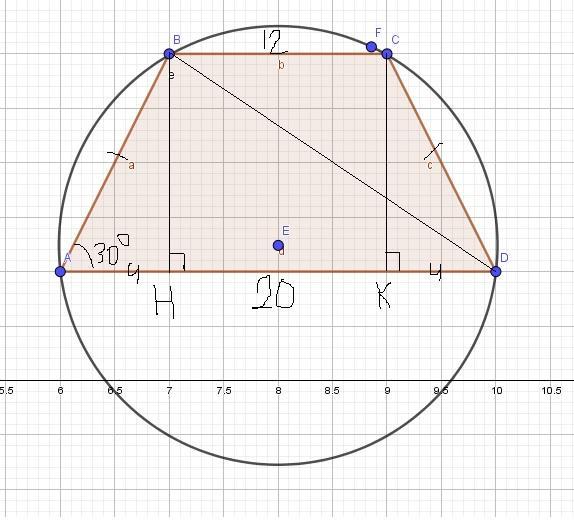
Нарисовал чертеж с обозначениями. Во-первых, описать окружность можно только около равнобедренной трапеции. Надо найти радиус этой окружности. Заметим, что окружность эта описана как около трапеции ABCD, так и около треугольника ABD.
Для треугольника ABD воспользуемся теоремой синусов и получим
То есть
Даже вот так. Радиус этой окружности равен длине стороны BD.
Осталось лишь её найти. Раз трапеция равнобедренная, то и прямоугольные треугольники ABH и DCK равны (по катету - высоте и гипотенузе - боковой стороне трапеции). Значит, AH = KD
Тогда AD = AH + HK + KD = 2*AH + HK
BCKH - прямоугольник, BC = HK = 12
AH = 0.5 * (AD - HK) = 0.5 * (20 - 12) = 4
HD = HK + KD = 12 + 4 = 16
Не хватает стороны BH. Её можно найти из треугольника ABH
Теперь по теореме Пифагора ищем BD
Ответ: