Предмет: Алгебра,
автор: polinafedko20
Помогите, пожалуйста!!!
Приложения:
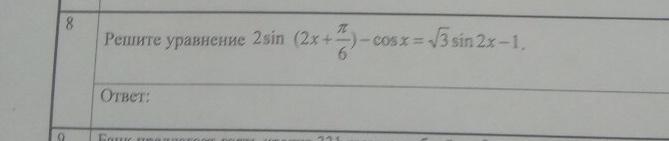
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Попробуем раскрыть синус суммы в левой части уравнения:
Раскроем косинус двойного угла:
Теперь рассматриваем два подуравнения:
Похожие вопросы
Предмет: Информатика,
автор: Camming
Предмет: Геометрия,
автор: Diana201992Youggg
Предмет: Қазақ тiлi,
автор: arturtajtakov38
Предмет: Литература,
автор: kdu48503
Предмет: Геометрия,
автор: dvddaria