Question

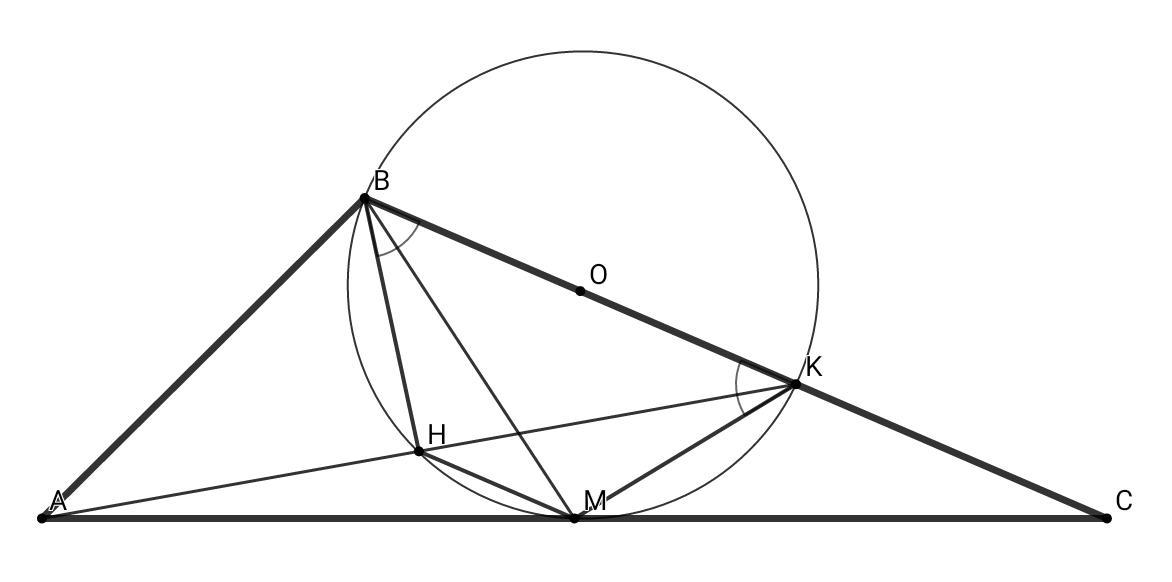
В треугольнике ABC точка M — середина AC. На стороне BC взяли точку K так, что угол BMK прямой. Оказалось, что BK = AB. Найдите ∠BKM, если ∠A + ∠C = 70
Номер 5

Answer 1

1 способ:  Опустим в ΔАВМ (АВ = ВК) высоту ВН ⇒ ВН⊥АК, АН = НК, но АМ = МС ⇒ НМ - средняя линия ΔАСК, НМ || ВС. Отрезок ВК из точек Н и М под прямым углом ⇒ четырёхугольник ВКМН вписанный, но НМ || ВК ⇒ ВКМН - равнобедренная трапеция, ВН = МК, ВМ = НК = АН, ∠ВКМ = ∠КВН = (180° - ∠А - ∠С)/2 = 55°

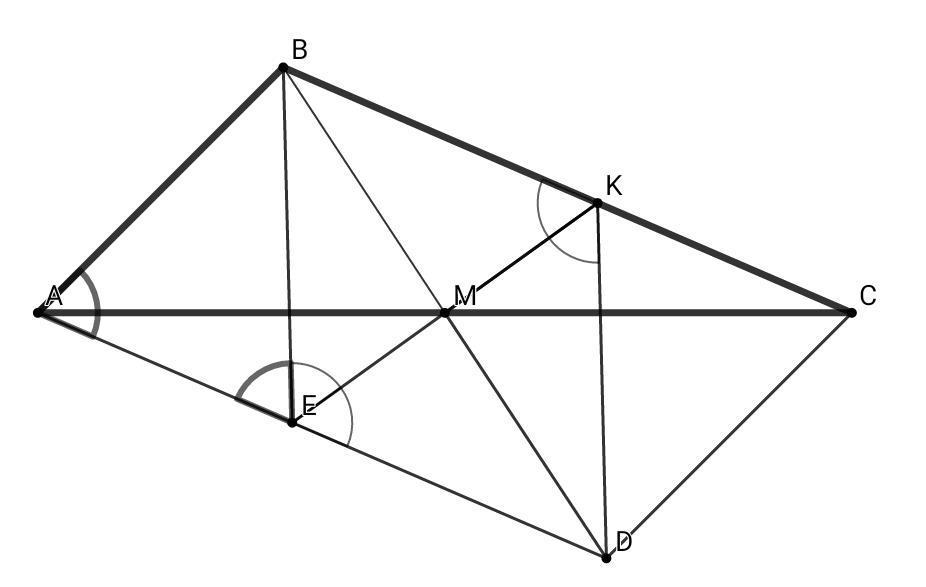
2 способ:  Удвоим медиану ВМ, достроив ΔАВС до параллелограмма АВСD, ЕК - серединный перпендикуляр к BD ⇒ BE = ED = DK = KB = AB = CD

∠BKM = ∠BED/2 = (180° - ∠AEB)/2 = (180° - ∠BAE)/2 = (180° - ∠A - ∠C)/2 = 55°

Ответ: 55°

Answer 2

Ответ:

Объяснение:В треугольнике ABC точка M