Question

Площадь основания прямоугольного параллелепипеда равна 48, а площади боковых граней 40 и 30. найдите площадь диагонального сечения ​

Answer 1

Ответ:

S = 50 ед².

Объяснение:

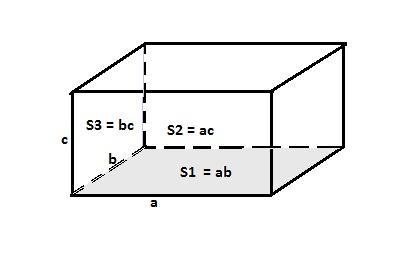
Пусть стороны прямоугольного параллелепипеда, образующие его измерения, равны "a", "b" и "c". Тогда площади основания и двух боковых граней равны

a·b = 48 (1), a·c = 40 (2) и b·c = 30 (3).

Выразим  сторону b из равенств (1) и (3) и приравняем полученное:

b = 48/a и b = 30/c  =>  48/a = 30/c  => c = 30a/48 = (5/8)a.

Подставим это значение в (2):

a·(5/8)a = 40  => a² = 320/5 = 64  =>  a = 8 ед.

Тогда из (1) b = 48/8 = 6 ед.  c = 30/8 = 5 ед. (из 2).

Найдем по Пифагору диагональ основания:

d = √(a²+b²) = √(64+36) = 10 ед.

Площадь диагонального сечения равна:

S = d·c = 10·5 = 50 ед².