Question

Докажите что окружность треугольника ABC бисектриса угла B и серединный перпендикуляр стороны AC проходят через одну точку. ТЕРМІНОВО!!!!!!!

Answer 1

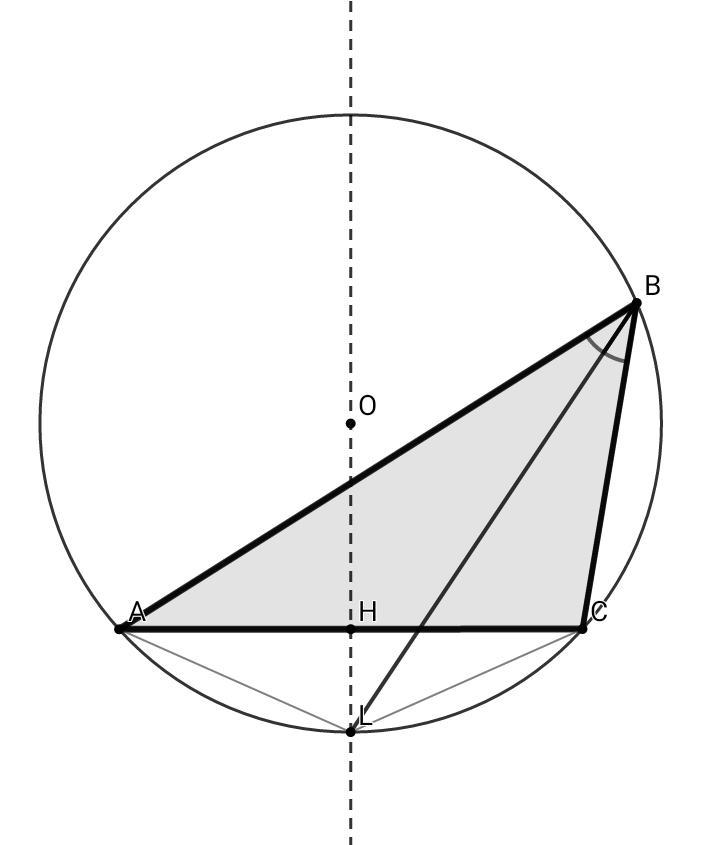
∠ABL = ∠CBL ⇒ UAL = ULC,  AL = LC - как хорды, опирающиеся на равные дуги, ΔALC - равнобедренный, высота которого является и медианой, и биссектрисой ⇒ LH⊥AC, AH = HC.

Биссектриса ∠В и серединный перпендикуляр к АС пересекаются в точке L, лежащей на описанной окружности ΔАВС.