Предмет: Алгебра,
автор: flo0809
Найдите сумму корней уравнения
Приложения:
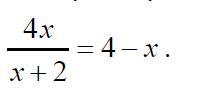
Ответы
Автор ответа:
1
Ответ:
-2
Объяснение:
Поделим с остатком левую часть уравнения, тогда получится
Это значит:
Дискриминант положительный (D = 36), значит есть два действительных корня, сумма которых (по теореме Виета) равна -2.
UPD:
Стоит иметь ввиду, что при x = -2 уравнение не имеет смысла, поэтому если какой-то корень уравнения = -2, то его не учитываем. В нашем случае такого нет, так как корни подбираются по теореме Виета очень легко: x1 = -4; x2 = 2
flo0809:
А не могли бы вы расписать как получили D=36
Похожие вопросы
Предмет: Литература,
автор: Voprosik017
Предмет: Литература,
автор: maksimsherbina201111
Предмет: Химия,
автор: kovedasofiia
Предмет: Математика,
автор: Marusevich01
Предмет: Литература,
автор: Darklehan12