Предмет: Алгебра,
автор: flo0809
Найдите наибольшее значение суммы , где решение системы x + y , где (x;y) решение системы {(х^2=3x+y и y^2=3y+x
Ответы
Автор ответа:
3
Ответ:
8
Объяснение:
Складывая данные уравнения , получим : x² +y² = 4(x+y) ( 1 )
пусть x + y = a ⇒ y = a-x , подставим в ( 1 ) вместо y ( a -x ) :
x² +( a-x)² - 4a = 0 или : 2x² -2ax +a²-4a = 0 ( 2 )
уравнение (2) имеет решение , если D/4 ≥ 0 или :
a² -2(a² -4a) ≥ 0 ⇔ a² -8a ≤ 0 ⇔ 0 ≤ a ≤ 8 ⇒ наибольшее a , при
котором уравнение ( 2 ) имеет решение равно 8 ⇒ a ≤ 8 ;
проверкой убеждаемся , что пара ( 4 ; 4) является решением
системы и мы доказали , что x+y ≤ 8 ⇒ 8 - наибольшее
значение суммы (x+y)
Приложения:
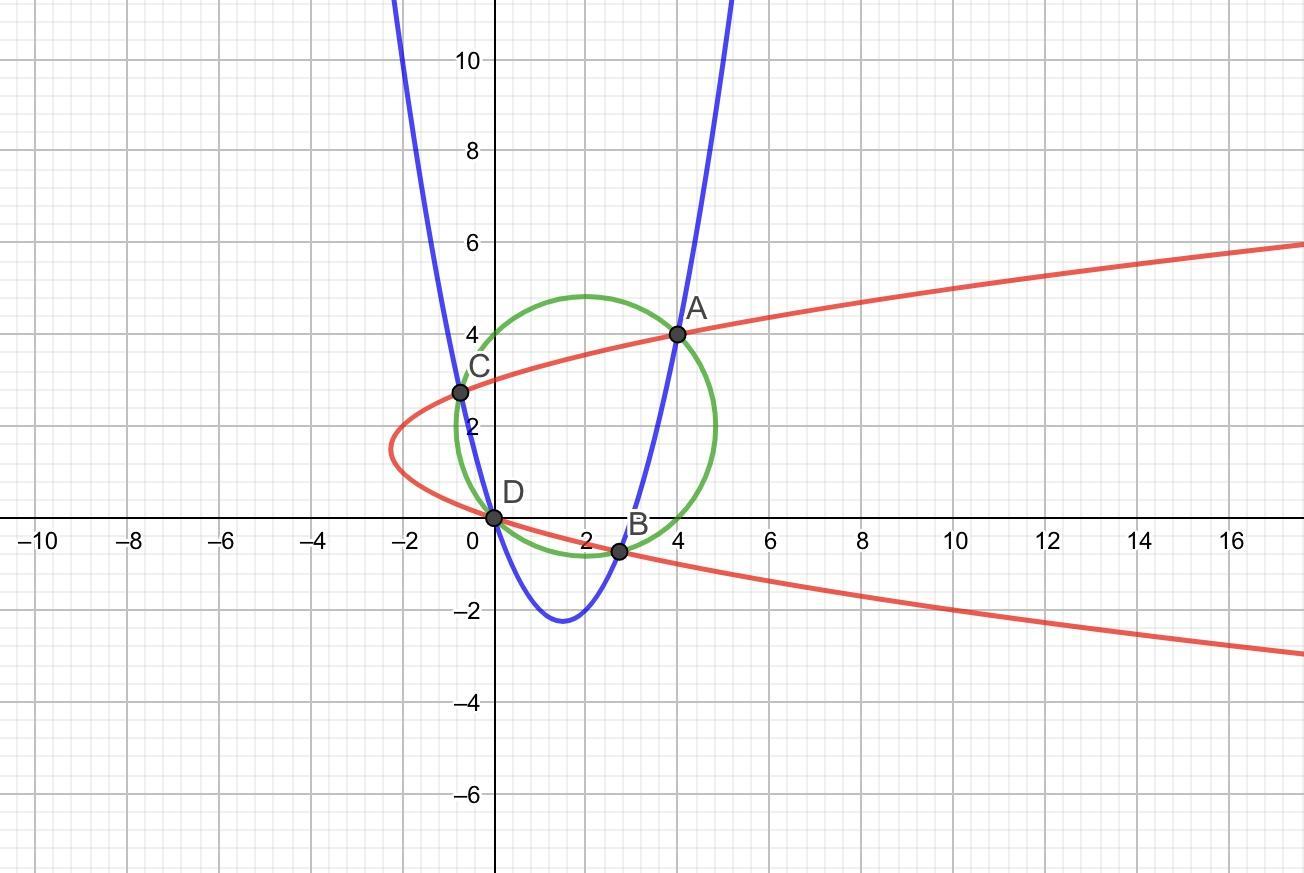
antonovm:
есть еще красивое геометрическое решение ( через окружность и касательную ) , но картинка не имеет к нему отношения , это иллюстрация ( не решение) , каждому решению системы соответствует одна из 4 точек пересечения двух парабол , как видно , наибольшая сумма координат ( 8 ) будет у точки А
x*z/(x+z)=xtz
tz*(x+3+t)=hx
hz*(x+6+z)=xzt
x+z=t*h
Найти значения всех букв (заменить цифрами) чтобы уравнение стало верным. Реши плизз
tz*(x+3+t)=hx
hz*(x+6+z)=xzt
x+z=t*h
Найти значения всех букв (заменить цифрами) чтобы уравнение стало верным. Реши плизз
Похожие вопросы
Предмет: Математика,
автор: ryze0iq
Предмет: Українська мова,
автор: molovnikita
Предмет: Французский язык,
автор: glebmarchukb
Предмет: Алгебра,
автор: idiot107
Предмет: История,
автор: скорпион36