ПОМОГИТЕ ПОЖАЛУЙСТА СРОЧНО!!!
Две окружности, касающиеся внешним образом, имеют общие внешние касательные КМ и КР, угол между которыми 90 ͦ. Хорды, соединяющие эти точки касания, равны

и

соответственно. Найдите расстояние между центрами окружностей.
Ответы
Ответ: Расстояние между центрами окружностей = 12
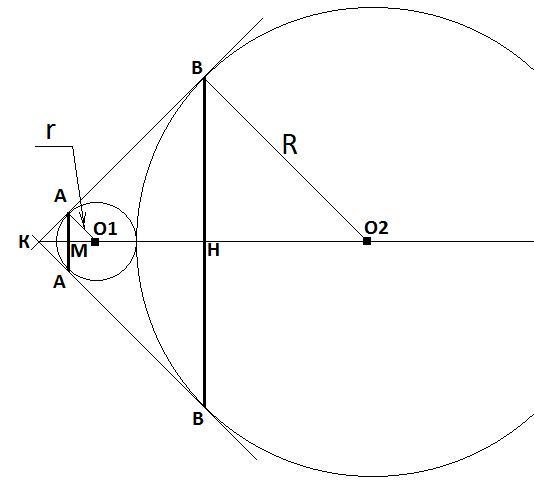
Объяснение: Смотрите рисунок.
К – точка пересечения касательных. Угол К – прямой. КО2 – биссектриса угла К. А и А, а так же В и В – точки касания окружностей касательных. АА и ВВ – хорды окружностей, пересекают биссектрису в точках М и Н соответственно. О1 и О2 – центры окружностей. На рисунке видно, что расстояние между центрами окружностей О1О2 = r + R. Найдем r. АО1 параллельна КА. Т.к КО1 – биссектриса угла К, то АА перпендикулярна КО1. Следовательно ∠КАМ = ∠МАО1 = 90/2 = 45° Т.к. ∠АМО1 = 90°, то ∠АО1М = 180 – 90 – 45 = 45°. Таким образом, ΔАМО1 – равнобедренный и О1М = АМ = (2√2)/2 = √2. Следовательно, r = √{(√2)² + (√2)²} = √4 = 2. Аналогично для R: О2Н = ВН = (10√2)/2 = 5√2. Тогда R = √{(5√2)² +(5√2)²} = √(25*2) + (25*2) = √100 = 10. Расстояние между центрами окружностей = 2 + 10 = 12