Предмет: Математика,
автор: sinicinaalesa
Постройте график функции у= (|х-4|+х+4) / х и определите, при каких значениях с прямая у=с будет иметь с графиком хотя бы одну общую точку.
Simba2017:
сложность в построении графика?
Ответы
Автор ответа:
1
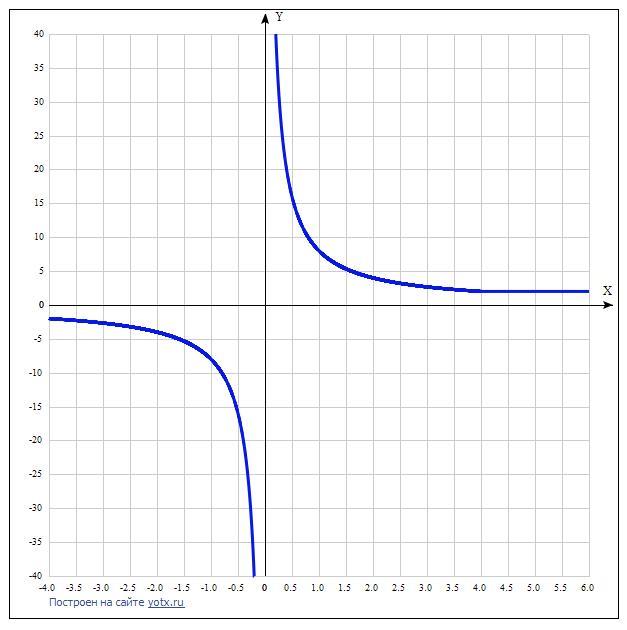
При x ≥ 4 график - прямая, проходящая через точку (0, 2) и параллельная оси абсцисс.
При x < 4 график - гипербола.
График см. во вложении.
Понятно, что при c ∈ [0; 2) прямая y = c не будет пересекать наш график. Значит, c ∈ (-∞; 0) ∪ [2; +∞).
Ответ: c ∈ (-∞; 0) ∪ [2; +∞).
Приложения:

Автор ответа:
1
Дана функция у= (|x-4|+x+4) / x.
Надо раскрыть модуль.
1) x > 4, у= (х-4+х+4) / х = 2x / x = 2 . Это прямая линия (делить на х можно).
2) x < 4, у=-х+4+х+4) / х = 8 / x .Это гипербола в 3-й четверти и в 1-й четверти от х = 0 до х = 4.
Область значений функции: у ∈ (-∞; 0) ∪ [2; +∞).
В этих же промежутках и будет прямая у=с будет иметь с графиком хотя бы одну общую точку.
Ответ: с ∈ (-∞; 0) ∪ [2; +∞).
Приложения:
А как мы понимаем, что при таких значениях с прямая будет иметь с графиком только одну общую точку?
Прямая у = с это прямая, параллельная оси Ох. Она пересекает график в одной точке (как минимум) в указанных промежутках.
Похожие вопросы
Предмет: Литература,
автор: xelio00052
Предмет: Геометрия,
автор: lbgvvfhnvfc
Предмет: Литература,
автор: dinislamova5678
Предмет: Литература,
автор: anita27072012