Предмет: Математика,
автор: lorya11123
Решить систему уравнений
Приложения:
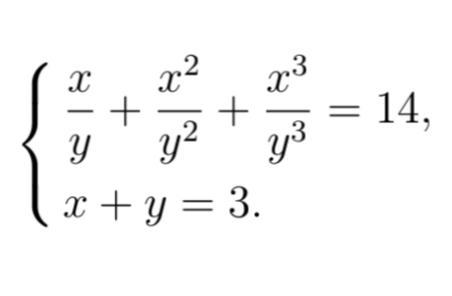
Ответы
Автор ответа:
1
Ответ: x=2 y=1.
Пошаговое объяснение:
Рассмотрим первое уравнение:
(x/y)+(x²/y²)+(x³/y³)=14
Пусть x/y=t ⇒
t+t²+t³=14
t³+t²+t-14=0
t³-4t²+4t+5t²-3t-14=0
t*(t²-4t+4)+5t²-3t-14=0
t*(t-2)²+5t²-3t-14=0
Разложим 5t²-3t-14 на множители:
5t²-3t-14=0 D=289 √D=17
t₁=2 t₂=-1,4 ⇒
5t²-3t-14=5*(t-2)*(t+1,4)=(t-2)*(5t+7)
t*(t-2)²+(t-2)*(5t+7)=0
(t-2)*(t*(t-2)+5t+7=0
t₁=2
t²-2t+5t+7=0
t²-3t+7=0 D=-19 ⇒ уравнение не имеет действительных корней.
t=x/y=2
{x=2y x=2*1=2.
{x+y=3 2y+y=3 3y=3 |÷3 y=1.
Похожие вопросы
Предмет: Алгебра,
автор: honeychiiik
Предмет: Английский язык,
автор: sofiapolisuk07
Предмет: Биология,
автор: KirillNeggr
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: nikitosu5