Предмет: Алгебра,
автор: netvoyager
найти значение выражения (2x^2 + y^2)/3xy если (x^2 - 4y^2)/xy =-3
Ответы
Автор ответа:
1
Если х = -4у, то
Если х = у, то
Ответ: -2,75; 1.
Приложения:
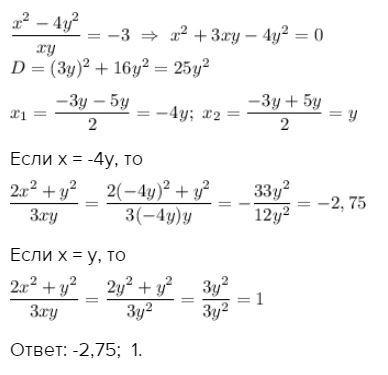
Похожие вопросы
Предмет: Литература,
автор: mixx19
Предмет: География,
автор: igorprocenko910
Предмет: Қазақ тiлi,
автор: noname2661
Предмет: Математика,
автор: nikitosu5