Предмет: Алгебра,
автор: nastenkakrupkoq
Алгебра. Упростить дробь. Задание на фото
Приложения:
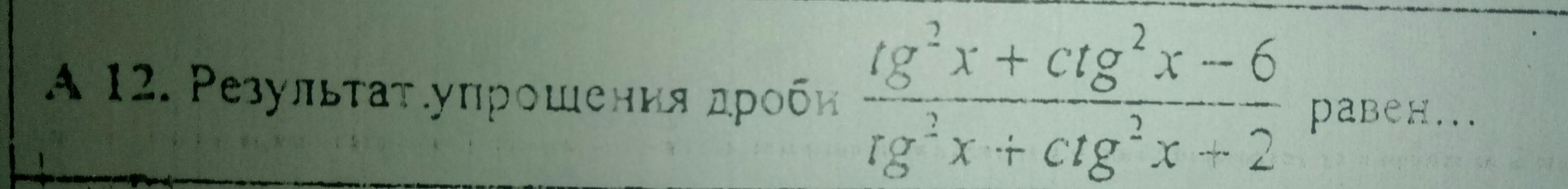
Ответы
Автор ответа:
0
Для начала отдельно выведем формулу для суммы квадратов тангенса и котангенса:
Переходим к основной задаче:
Ответ: cos4x.
Похожие вопросы
Предмет: Информатика,
автор: kulikanna2008
Предмет: Биология,
автор: a9108166669
Предмет: Английский язык,
автор: dianazavadka303
Предмет: Математика,
автор: YulaBraun
Предмет: Литература,
автор: uralbendi