Предмет: Математика,
автор: Grishan4ik1
Помогите решить, пожалуйста
Приложения:
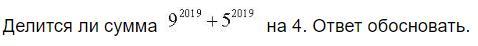
Simba2017:
я думаю нет
Ответы
Автор ответа:
1
Ответ:
нет
Пошаговое объяснение:
9^2019 - 5^2019. Делится ли это число на 4?
Число делится на 4, если две последние цифры образуют число, которое делится на 4.
Знак = будет означать "имеет такой же остаток при делении на 4".
9 в нечетной степени кончается на 9, а в четной степени на 1.
9^2019 = 9
Последние две цифры в степени ходят по кругу:
9^1 = 09; 9^3 = 29; 9^5 = 49; 9^7 = 69; 9^9 = 89; 9^11 = 09.
5 в любой степени кончается на 25.
Сложим окончания чисел:
09 + 25 = 34
29 + 25 = 54
49 + 25 = 74
69 + 25 = 94
89 + 25 = 114
Все эти числа не делятся на 4. Значит, при любых двух последних цифрах в числе 9^2019 сумма не будет делиться на 4.
в условии же сумма
ошибся, поправил
Спасибо большое , не могли бы вы решить аналогичные задачи которые есть у меня в профиле ?
Автор ответа:
1
9²⁰¹⁹ + 5²⁰¹⁹ ≡ 1²⁰¹⁹ + 1²⁰¹⁹ = 1 + 1 = 2 (mod 4). ⇒ 9²⁰¹⁹ + 5²⁰¹⁹ не кратно 4.
Ответ: нет.
Похожие вопросы
Предмет: Математика,
автор: ellizzas
Предмет: Русский язык,
автор: kurvanzanhodzasev209
Предмет: Французский язык,
автор: yyaau74
Предмет: Математика,
автор: Epic23232323