ДАЮ 98 БАЛОВ ЗА 3 ЗАДАЧИ
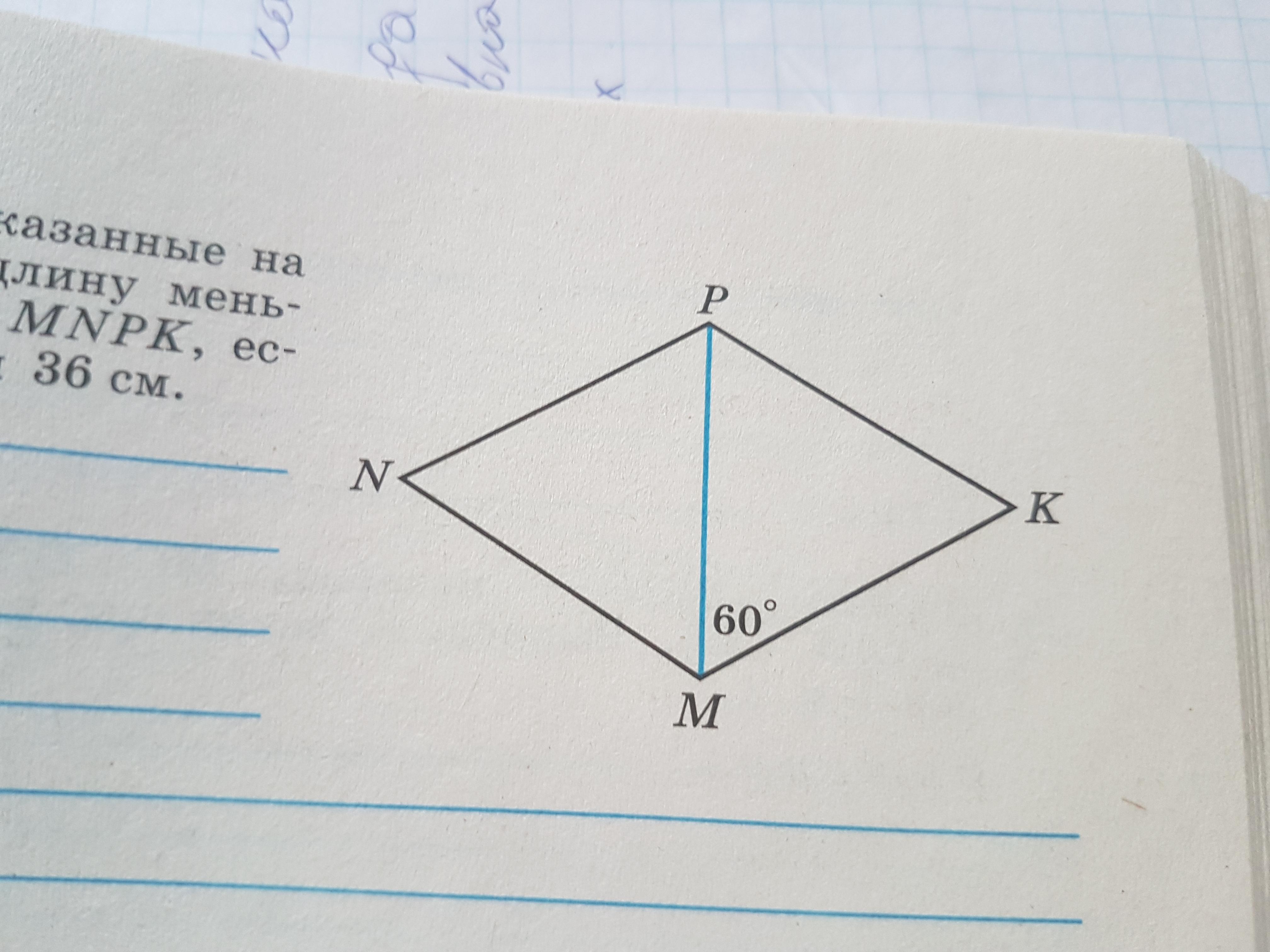
1. Используя данные указаны на рисунке вычислите длину меньшей диагонали ромба mnpq если его периметр равен 36 см.(Рисунок внизу)
2. Периметр квадрата равен 80 см середины 2 его противоположных сторон соединены отрезком вычислите сумму периметров 2 образовавшихся четырехугольников.
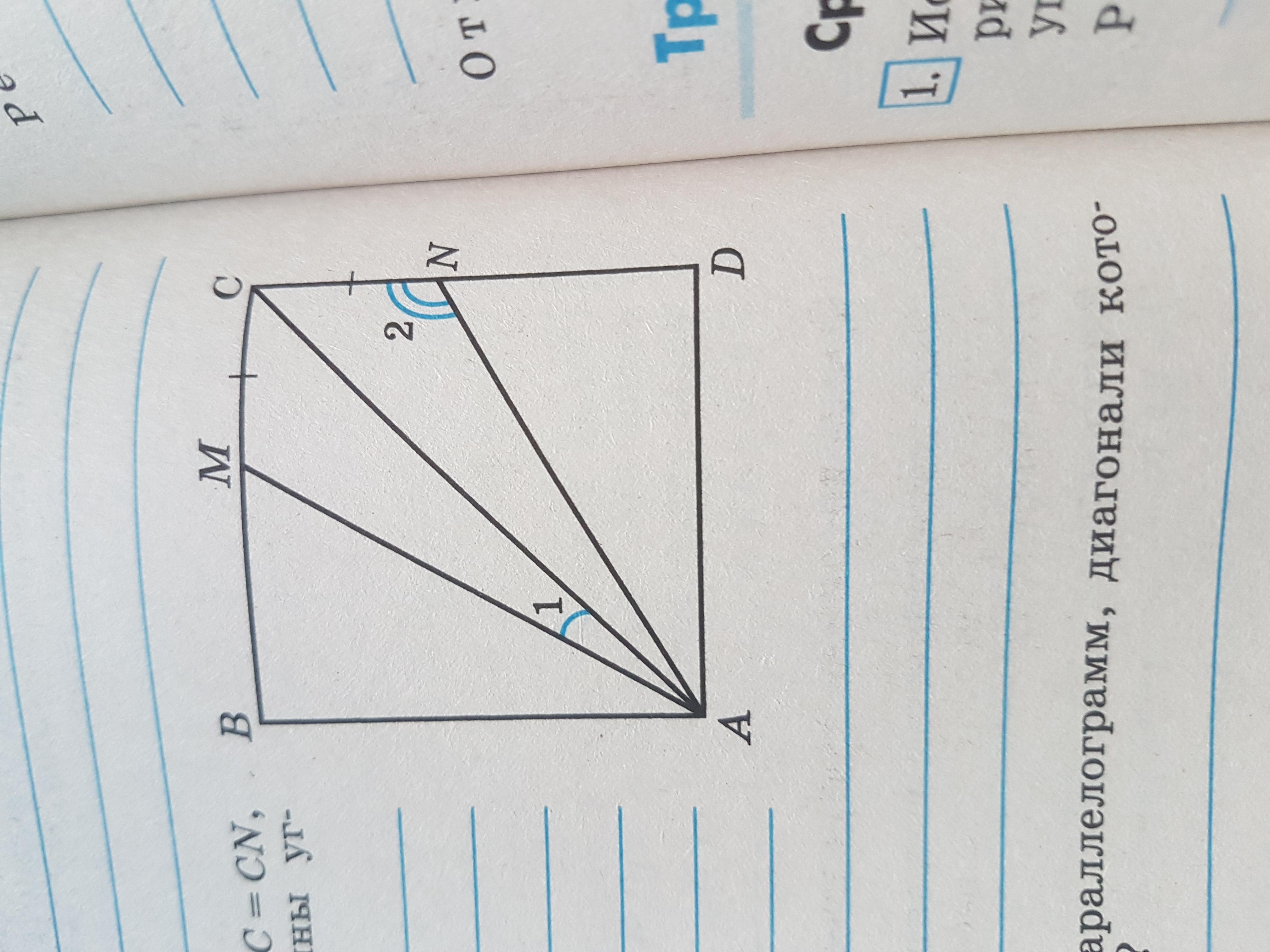
3. ABCD-квадрат, MC=CN, угол MAN=32 градуса. Вычислите величины углов 1 и 2.(Рисунок внизу)
Ответы
Ответ:
Объяснение:
1) диагональ ромба является биссектрисой углов⇒ если ∠PMK=60, то ∠NMK=120, а углы ромба N и K=60 Итак, в ΔPMK все углы по 60⇒он равностор. и МР=9
периметр равен 36 см⇒сторона ромба=36:4=9
2) Сторона квадрата 80:4=20
периметр одного прямоугольника Р=20+10+20+10=60 2*Р=120см
Ответ.
1) Если периметр ромба, у которого все стороны равны, равен 36 см, то сторона ромба равна 36:4=9 см.
Рассмотрим ΔМРК. Он равнобедренный, т.к. РК=МК=9 см и один из углов равен 60° ( ∠РМК=60° ). Значит этот треугольник равносторонний и сторона РМ=9 см. Но РМ - это меньшая диагональ ромба.
Ответ: 9 см .
2) Периметр квадрата = 80 см. Так как все стороны квадрата равны, то сторона квадрата = 80:4=20 см.
Соединим середины противоположных сторон квадрата отрезком, получим два прямоугольника со сторонами 20, 10, 20 , 10. Периметр одного такого прямоугольника Р=20+10+20+10=60 см. А сумма периметров двух одинаковых прямоугольников равна 60*2=120 см .
3) АВСД - квадрат , все его углы = 90°, а диагональ делит углы квадрата пополам, то есть ∠АСМ=∠ACN=90°:2=45° .
МС=NC , ∠MAN=32° .
ΔАМС=ΔANC по 1 признаку, так как МС=NC , ∠ACM=∠ACN , АС - общая сторона ⇒ ∠МАС=∠NAC=32°:2=16° ⇒ ∠1=16° .
Рассм. ΔАСN . ∠2=180°-∠NAC-∠ACN=180°-16°-45°=119° .