Пожалуйста, помогите решить задание 18 на фото?
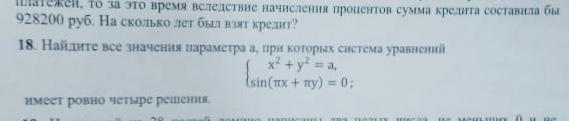
Ответы
Ответ: a=1/2
Подробное решение: в закрепе. Извините за аналитический подход, не смог обойтись без него.

Введем систему координат x, y. Тогда - уравнение, задающее окружность, радиуса
, с центром в начале координат.
Из второго уравнения следует . То есть на графике это серия прямых. Одна из прямых проходит через начало координат. Это уже два решения (случай
не имеет смысла рассматривать). Остальные прямые, пересекающие окружность, симметричны относительно первой прямой, а, значит, решений будет 6. Единственная возможность иметь ровно 4 решения - иметь две прямые, касающиеся окружности. Поскольку прямые имеют наклон 45 гр. к оси абсцисс, то очень просто найти координаты пересечения этих прямых с осью ОХ. Сделав это, получаем
; Значит искомое множество A можно задать так: