Предмет: Алгебра,
автор: nnnn69
решить неравенство.
Приложения:
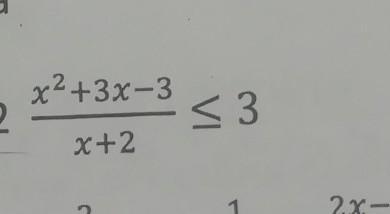
Ответы
Автор ответа:
1
Ответ:
x^²+3x-3
/ x+2
Объяснение:
x^2 +2x + x - 3
/x+2
(x+2)x+x-3
/x+2
2x-3 відомі вправо невідомі вліво і вийде не забуваємо змінити знак 2x≤6
x≤3
Автор ответа:
1
Ответ: x ∈ (-∞; -3] ∪ (-2; 3] .
Решение:
Преобразуем выражение:
Теперь отметим на координатной прямой все x, дающие нули в скобках (все точки, кроме дающей 0 в знаменателе, то есть, кроме -2 , закрашенные, а -2 - выколотая) и отметим нужные знаки:
-∞ - - - -3 + + + -2 - - - 3 + + + +∞
Нам нужны именно промежутки, где значение меньше нуля, поэтому:
x ∈ (-∞; -3] ∪ (-2; 3] .
matilda17562:
Описка в пятой строке. В числителе дроби х^2 - 3^2, у Вас 9^2. Исправьте, пожалуйста.
Похожие вопросы
Предмет: Алгебра,
автор: vsmisleneverniynik
Предмет: Қазақ тiлi,
автор: zxcursedstudent
Предмет: Биология,
автор: alisamalkova
Предмет: Биология,
автор: plkjhgfdsaq