Докажите, что уравнения не имеют корней.
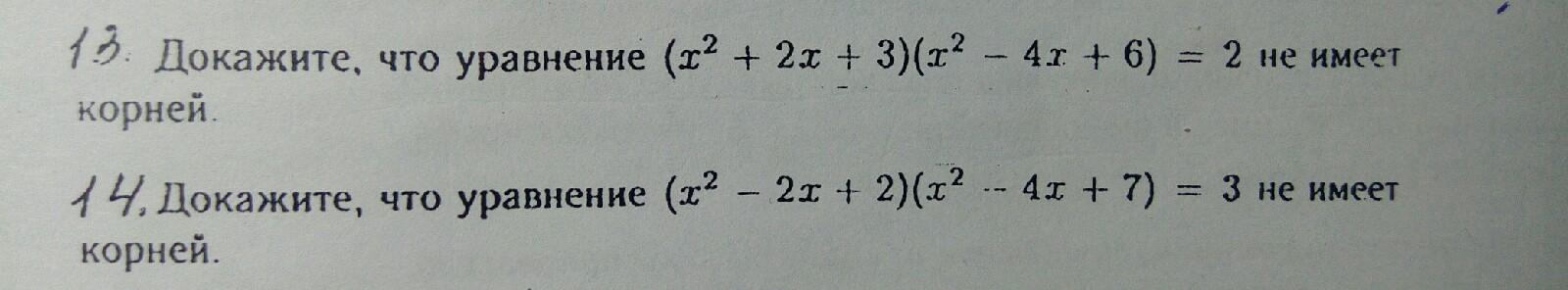
Ответы
Ответ:
Пошаговое объяснение:
13. Квадратный трёхчлен в первой скобке: (х + 1)² + 1 при любом значении х больше 1 (значение х = -1 исключаем, поскольку при нём вторая скобка больше 2). Квадратный трёхчлен во второй скобке: (х - 2)² + 2 при любом значении х больше 2 (значение х = 2 исключаем, поскольку при нём первая скобка всегда больше 1. Таким образом, в левой части уравнения мы имеем произведение двух сомножителей, первый из которых всегда больше 1, второй - всегда больше 2. Значит, произведение всегда больше 2 и ни при каких значениях переменной не равно 2. Ч.т.д.
Доказательство:
1. (х^2 + 2х + 3)(х^2 - 4х + 6) = 2
а) Рассмотрим первый множитель:
х^2 + 2х + 3 = х^2 + 2х + 1 + 2 = (х + 1)^2 + 2.
Так как (х + 1)^2 ≥ 0 при всех действительных значениях х, то
(х + 1)^2 + 2 ≥ 2.
б) Рассмотрим второй множитель:
х^2 - 4х + 6 = х^2 - 4х + 4+ 2 = (х - 2)^2 + 2.
Так как (х - 2)^2 ≥ 0 при всех действительных значениях х, то
(х - 2)^2 + 2 ≥ 2.
в) Получим, что
(х^2 + 2х + 3)(х^2 - 4х + 6) ≥ 2•2
(х^2 + 2х + 3)(х^2 - 4х + 6) ≥ 4, а значит произведение равным двум быть не может, уравнение
(х^2 + 2х + 3)(х^2 - 4х + 6) = 2 корней не имеет.
1. (х^2 + 2х + 2)(х^2 - 4х + 7) = 2
а) Рассмотрим первый множитель:
х^2 + 2х + 2 = х^2 + 2х + 1 + 1 = (х + 1)^2 + 1.
Так как (х + 1)^2 ≥ 0 при всех действительных значениях х, то
(х + 1)^2 + 1 ≥ 1.
б) Рассмотрим второй множитель:
х^2 - 4х + 7 = х^2 - 4х + 4+ 3 = (х - 2)^2 + 3.
Так как (х - 2)^2 ≥ 0 при всех действительных значениях х, то
(х - 2)^2 + 3 ≥ 3.
в) Получим, что
(х^2 + 2х + 3)(х^2 - 4х + 6) ≥ 1•3,
(х^2 + 2х + 3)(х^2 - 4х + 6) ≥ 3, а значит произведение равным двум быть не может, уравнение
(х^2 + 2х + 3)(х^2 - 4х + 6) = 2 корней не имеет.