Question

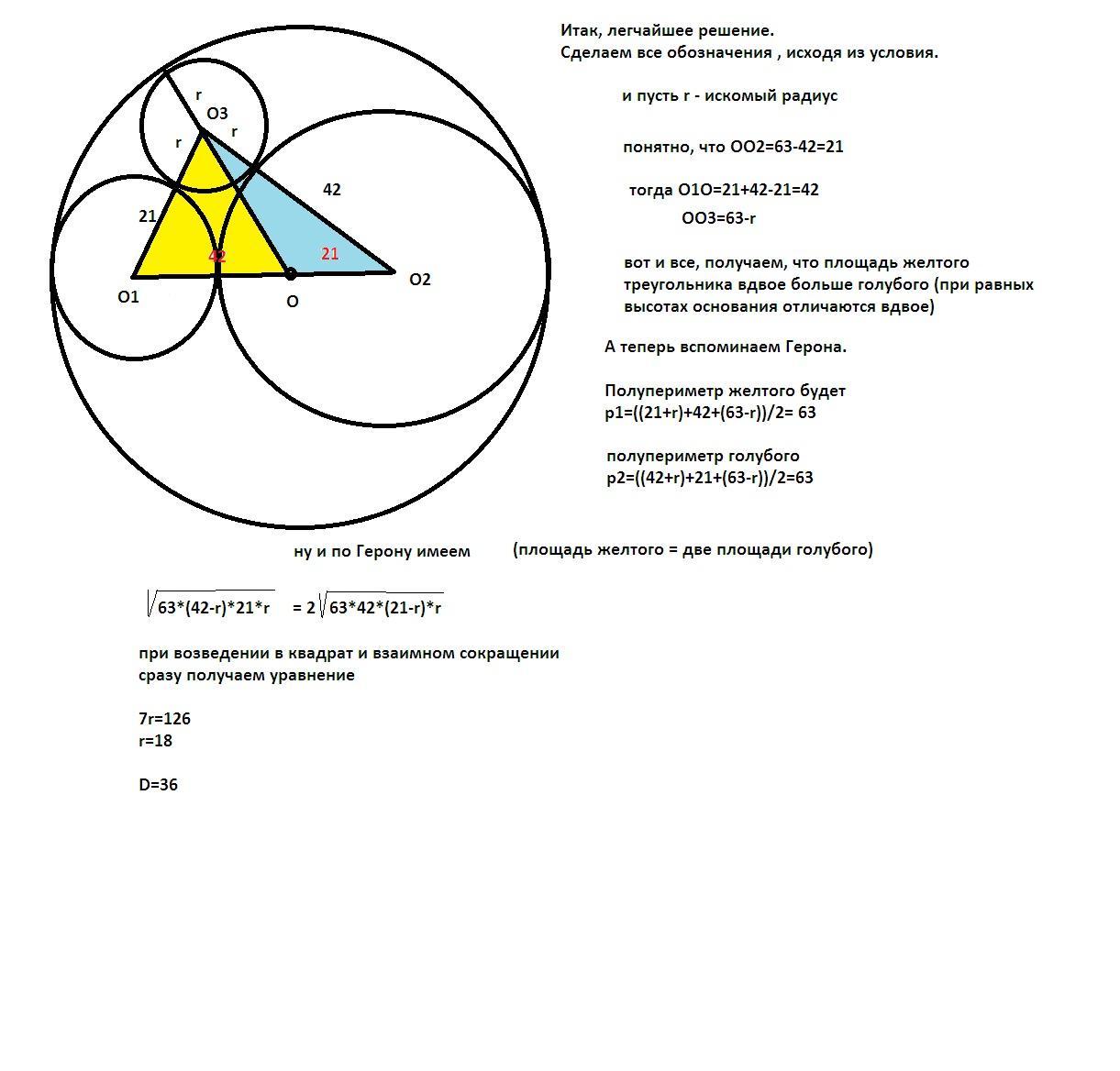
В окружность диаметра 126 вписаны 2 окружности диаметров 84 и 42. Окружность какого наибольшего диаметра можно вписать в большую окружность таким образом, чтобы она касалась внутренних окружностей внешним образом?

АВ = 126
АС = 42
ВС = 84
D,E,F - точки касания
Диаметр красной окружности?

Answer 1

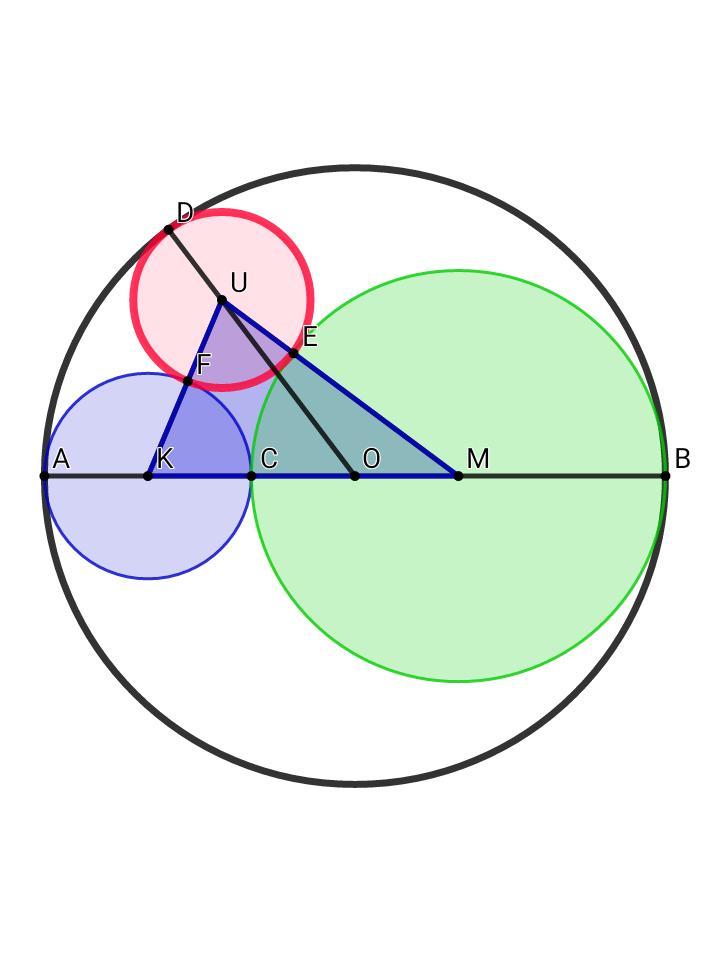
Пусть радиус красной окружности R = x, тогда КМ = KC + CM = 21 + 42 = 63, KU = FU + KF = x + 21, MU = UE + ME = x + 42, UO = DO - DU = 63 - x

Применим теорему косинусов для ΔКМU:

KU² = KM² + UM² - 2•KM•UM•cos∠KMU

(x + 21)² = 63² + (x + 42)² - 2•63•(x + 42)•cos∠KMU

x² + 42x + 441 = 3969 + x² + 84x + 1764 - 126•(x + 42)•cos∠KMU

126•(x + 42)•cos∠KMU = 42x + 5292  ⇒  cos∠KMU = (x+126)/3(x+42)

Теперь ещё раз применим теорему косинусов уже для ΔUOM:

UO² = OM² + UM² - 2•OM•UM•cos∠OMU

(63 - x)² = 21² + (x + 42)² - 2•21•(x + 42)•cos∠OMU

x² - 126x + 3969 = 441 + x² + 84x + 1764 - 42•(x + 42)•cos∠OMU

42•(x + 42) = 210x - 1764 ⇒ cos∠OMU = (5x - 42)/(x + 42)

cos∠KMU = cos∠OMU ⇒ (x + 126)/3(x + 42) = (5x - 42)/(x + 42)

x + 126 = 3•(5x - 42) ⇔ 14x = 252 ⇔ R = x = 18 ⇒ D = 36

Ответ: 36

Answer 2

Ответ:

Решение смотри в файле

Объяснение: