Предмет: Математика,
автор: brucelee2020
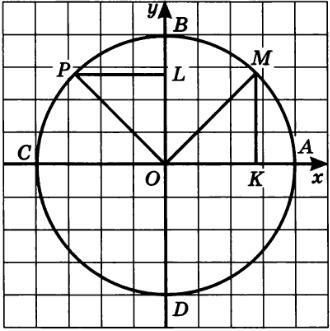
Почему тут дуга AM равняется дуге PB?
(точке M соответствует число t, а точке P - число t + pi / 2)
помогите плис <3
Приложения:
LFP:
угол АОМ = t; угол АОР = (пи/2)+t; следовательно, угол РОВ = t... центральные углы равны, значит и дуги равны...
почему угол POB равняется t? там же еще неизвестный угол BOM появляется?
угол ВОМ нас не интересует
или угол ВОМ = (pi/2)-t
угол РОВ = t по условию: точке Р соответствует число t+(pi/2)
угол АОВ = pi/2...если его вычесть из угла АОР, останется только t...
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
По условию /_POM=90°
Также /_BOK=90°
Значит /_МОА=/_РОВ, как дополняющие один и тот же угол /_ВОМ до 90°.
Значит дуга АМ равна дуге РВ, как опирающиеся на равные углы.
Похожие вопросы
Предмет: История,
автор: dilnazomarkanova
Предмет: Қазақ тiлi,
автор: tmama4507
Предмет: Английский язык,
автор: asylzhanzhanibekkyzy
Предмет: Литература,
автор: Yan1201