Question

В окружности проведены хорды АВ и АС, причем АВ=2, ВС=1, угол САВ равен 120°. Найти длину той хорды, которая делит угол САВ пополам.

Answer 1

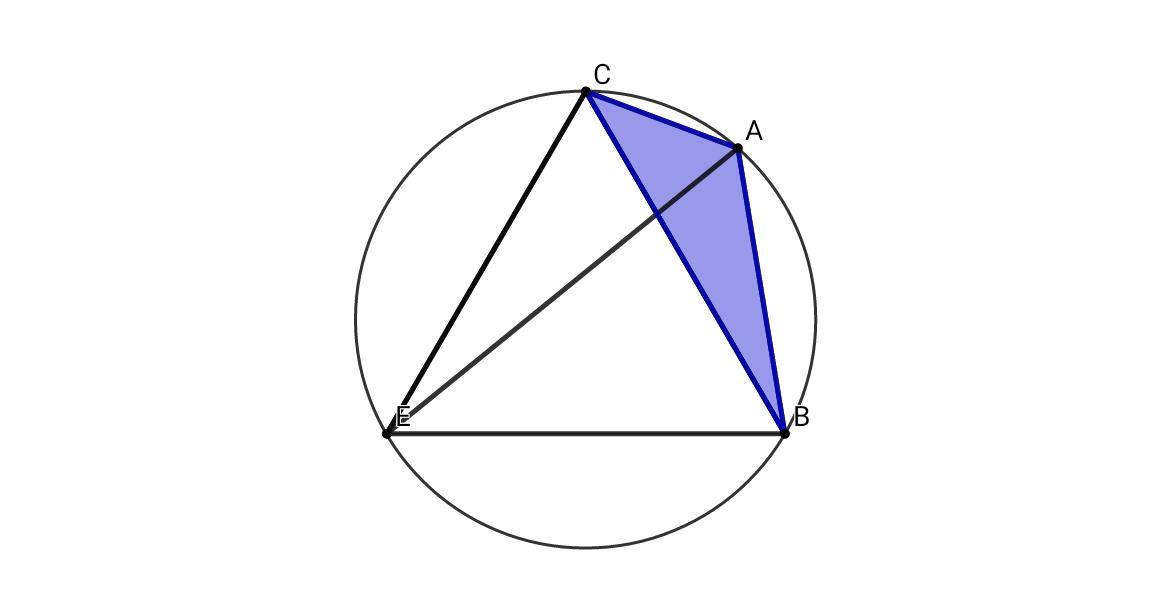
АВЕС - вписанный четырёхугольник ⇒ ∠ВЕС = 180° - 120° = 60°

∠САЕ = ∠ВАЕ = 60° ⇒ СЕ = ВЕ - как хорды, опирающиеся на равные дуги ⇒ ΔВЕС - правильный, ВС = СЕ = ВЕ

По теореме косинусов для ΔАВС и ΔАВЕ:  ВС² = ВЕ²

АВ² + АС² - 2•АВ•АС•сos120° = AB² + AE² - 2•AB•AE•cos60°

1 - 2•2•(-1/2) = AE² - 2•2•AE•(1/2) ⇒ AE² - 2AE - 3 = 0 ⇒ AE = 3 - по теореме, обратной т.Виета, второй корень не подходит.

Ответ: 3