Предмет: Математика,
автор: havfsq
Помогите найти предел последовательности, с решением
Приложения:
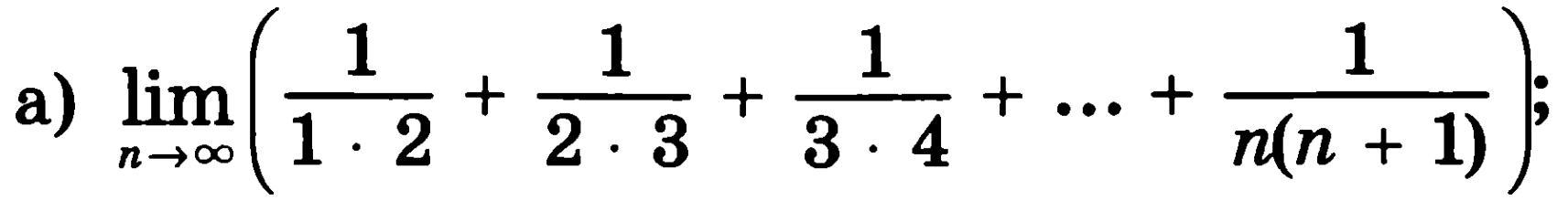
Ответы
Автор ответа:
1
Ответ 1. Решение задания приложено
Приложения:

Аноним:
Здорово!
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Математика,
автор: ceylin37
Предмет: Физика,
автор: GeraldWhateWolf
Предмет: Английский язык,
автор: aruzhankairdinova
Предмет: Математика,
автор: AYS14
Предмет: Математика,
автор: Аноним