Предмет: Алгебра,
автор: prilfomer
Решите неравенство пожалуйста.
Приложения:
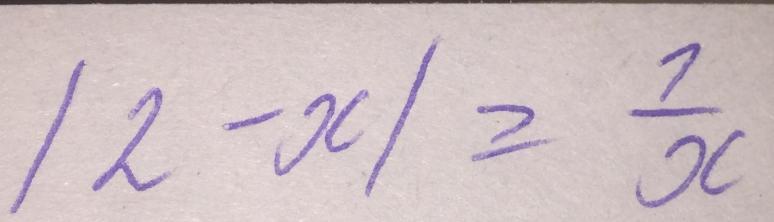
Ответы
Автор ответа:
1
+ - +
_________[1 - √2]___________[1 + √2]___________
////////////////////// ///////////////////////////
Ответ : (- ∞ ; 1 - √2] ∪ [1] ∪ [1 + √2 ; +∞)
antonovm:
вы в решении 2 раза домножали на х и при этом знак не менялся , а если х <0 ? и все отрицательные х должны войти в ответ ( модуль больше любого отрицательного числа ) , а у вас в ответе не так
Не обязательно знак будет меняться, но правильный отрезок (-∞;0)U{1}U[1 + √2 ; +∞)
так в решении он и не меняется , то есть подразумевается , что х - положительный , а он не обязан быть таким и из вашего ответа ( верного) это видно
Похожие вопросы
Предмет: Обществознание,
автор: arianagarmaevs
Предмет: Обществознание,
автор: arianagarmaevs
Предмет: Алгебра,
автор: lastepsey
Предмет: Математика,
автор: anita27072012
Предмет: Химия,
автор: elvinio2010