Question

Решите, пожалуйста, задачу 3 уровня по геометрии
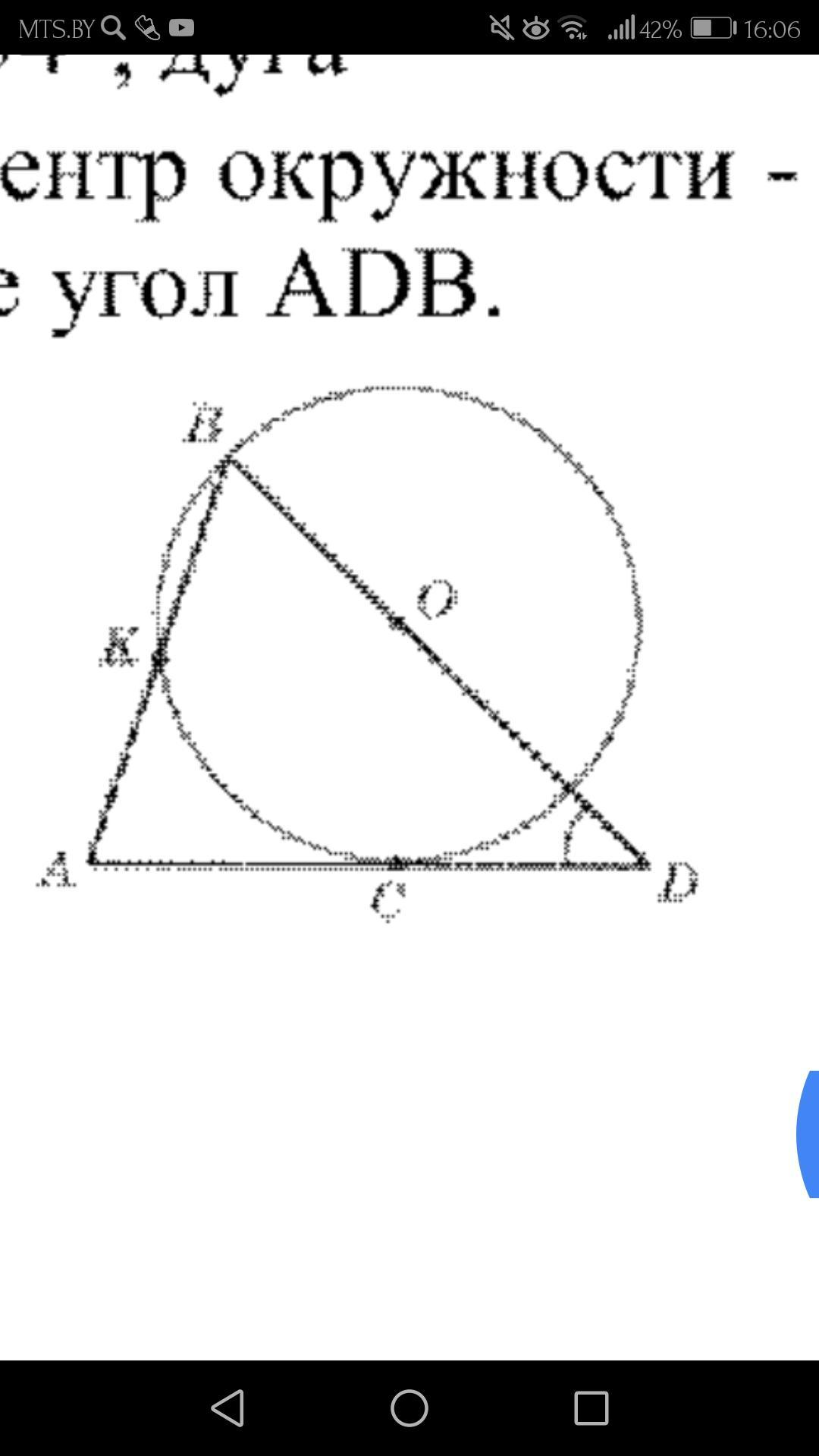
АС-касательная, дуга ВК содержит 54°, дуга КС-82°, центр окружности - точка О, Найдите угол АDB.

Answer 1

Ответ:

Объяснение:   АС-касательная, АВ-секущая угол между ними ∡ВАС=(большая дуга ВС-дугаКС):2

большая дуга ВС=360-(54+82)=224    дугаКС=82

∡ВАС=(224-82):2=71

Из ΔАВД  искомый ∡АДВ=180-(64+71)=45

Answer 2

Ответ: 46°

Объяснение:

центральный угол ВОС = 54°+82° = 136°, следовательно, смежный ему угол COD = 180°-136° = 44°;

радиус, проведенный в точку касания, перпендикулярен касательной, угол OCD = 90°

из прямоугольного треугольника OCD угол ODC = 90°-44° = 46° = углу ADB