Предмет: Математика,
автор: avdeevam185
Помогите пожалуйста решить задачу по геометрии! Без использования тригонометрические функций!
Приложения:

Ответы
Автор ответа:
0
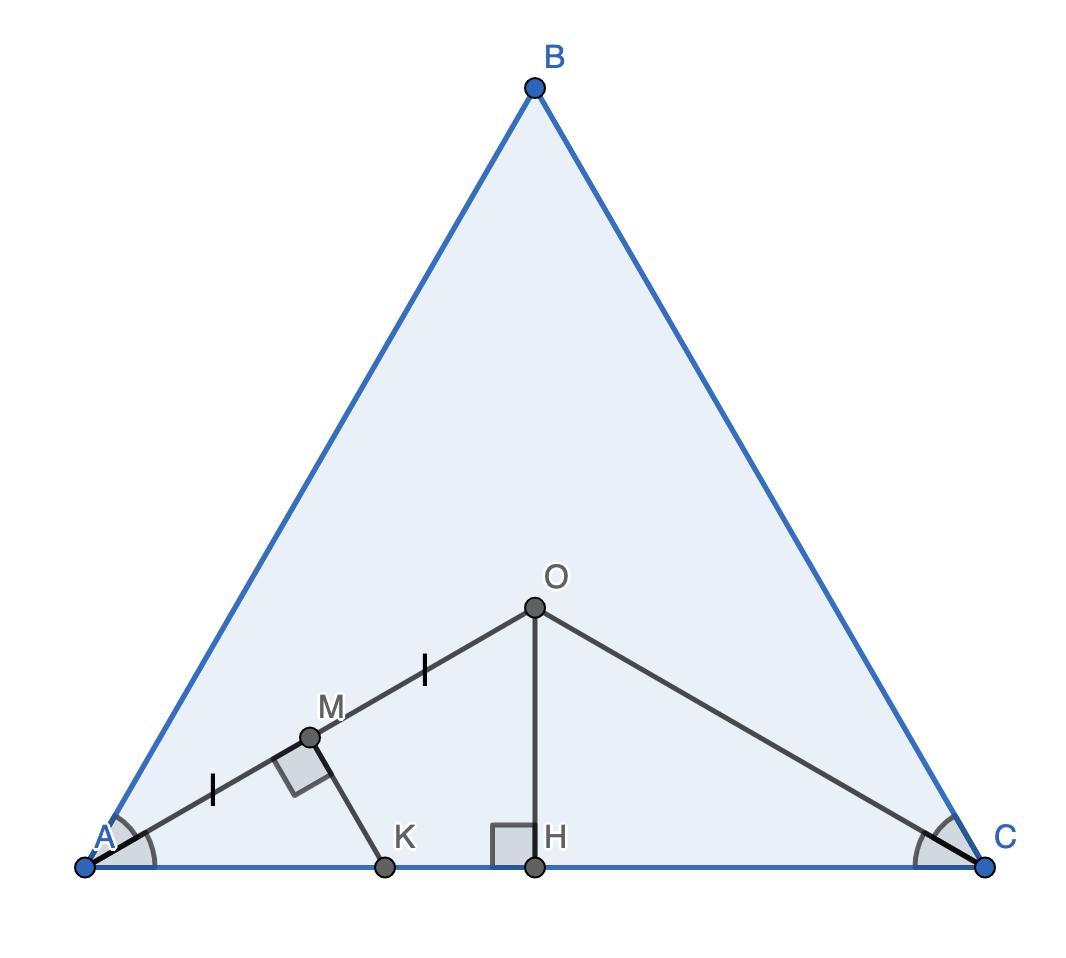
Проведём перпендикуляр OH к AC.
Рассмотрим ΔAMK и ΔAHO:
- ∠OAH — общий;
- ∠AMK = ∠AHO = 90° ⇒
⇒ ΔAMK ~ ΔAHO по двум углам ⇒
ΔAOC — равнобедренный, OH ⊥ AC ⇒ AH = HC ⇒ AH = AC : 2 = 3.
O — центр пересечения биссектрис, но ΔABC — правильный ⇒ O — точка пересечения медиан (которые в правильном треугольнике равны, как бы их ни проводили; обозначим медиану за m) ⇒ . Но в правильном треугольнике медиана — это ещё и высота, значит,
.
Ответ: AK = 2 см, KC = 4 см
Приложения:
avdeevam185:
Есть ли способ решить без подобия, тригонометрии, т. Пифагора? Мы этого ещё не проходили
Похожие вопросы