Здравствуйте, возьмём простейшее уравнение sin x = 1. Его корень таков: x=π/2+2πk, k€Z (это так называемый частный случай). Теперь решим это же уравнение, воспользовавшись общей формулой корней синуса. Получим после использования данной формулы следующий корень: x=(-1)^n×arcsin(1)+πk => (-1)^n×π/2+πk.
Мой, собственно, вопрос: куда из корня уравнения частного случая делась (-1)^n и откуда в нём появилась двойка перед πk, ведь в общей формуле её нет? Объясните, пожалуйста, связь между частным случаем корня и общим (если она существует, конечно...).
Ответы
Ответ:
Объяснение:
Смотри, значит. При нечетных n получим, что первое слагаемое отрицательно, т. е. находится на оси sin(x) между III и IV четвертями. Прибавляя нечетное число π, получаем точку сверху, как раз ту, которая является решением.
Теперь возьмем n четное. Первое слагаемое положительно, а так же получаем некоторое четное количество оборотов (четное число π), которое возвращает нас в эту же точку, так как является периодом функции sin(x)
Объяснение:
Конечно же обе формулы дают ОДНИ И ТЕ ЖЕ решения. Просто запись в частном случае более лёгкая для восприятия.
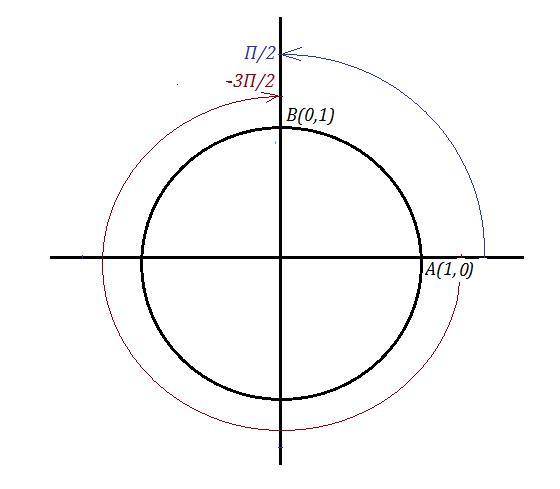
Из этой формулы следует, что sinx=1 при х=П/2 , причём, если эту точку повернуть на один круг (+/-2П), два круга (+/-4П), три круга (+/-6П) и так далее, то придём в одну ту же точку В на тригонометрическом круге с декартовыми координатами (0,1) . Смотри рисунок. Поворачивать точку можно против часовой стрелки ( ) или по часовой стрелкe (
) .
В случае общей формулы надо рассматривать чётные и нечётные значения .
Если k- чётно, то получаем
То есть получили ту же формулу, что и в частном случае.
Если k - нечётно, то получаем
На вид эта формула не похожа на частный случай, но точка х= -3П/2 получается из точки с дек. координатами А(1,0) путём её поворота на 270° (3П/2) по часовой стрелке (отрицательное направление поворота, поэтому знак (-) пишем ). И попадёт она в точку В(0,1). Но ведь мы попадём в точку В(0,1) и при повороте точки А(1,0) против часовой стрелки ( положительное направление поворота) на 90° (П/2) .
Поэтому запись равноценна записи
.
Конечно, предпочтительнее сразу писать частный вид формулы для решения уравнения sinx=1, потому что он более простой в записи , но описывает те же решения, что и частный случай.