Сколькими способами можно раскрасить клетки прямоугольника 2*2019 в два цвета так чтобы никакие три клетки одного цвета не образовали уголок из трёх клеток ?
Ответы
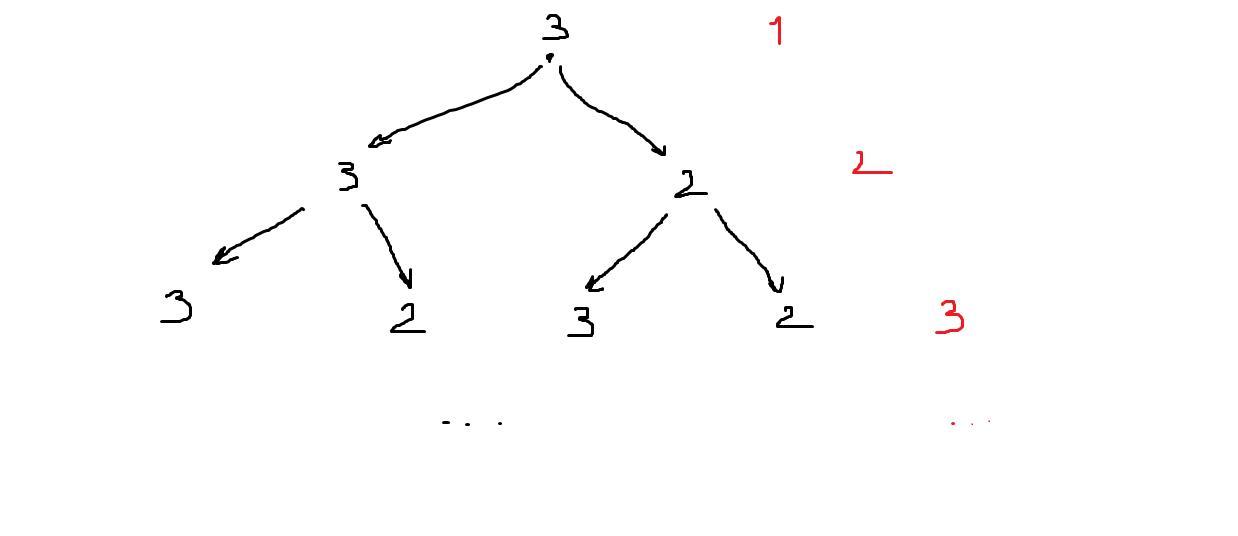
Пусть мы красим в белый и черные цвета. Заметим, что в любой правильной раскраске должно быть поровну обоих цветов. Иначе в каком-нибудь квадрате 2x2 найдется три клетки одного цвета, что невозможно. Теперь будем по порядку рассматривать квадраты 2x2. Пусть изначально прямоугольника покрашен в шахматную расцветку. Для того, чтобы получать новую раскраску будем двигать черные (без ограничения общности - двигая черные мы, грубо говоря, двигаем и белые) клетки (в квадратах, двигаясь слева направо), причем так, чтобы не возникало уголков. Действительно, если они будут возникать, то их придется устранять и тем самым создавать их в квадратах, расположенных правее и в конце концов упремся. Таким образом, для первого квадрата существует три движения (включая тождественную перестановку). Для второго квадрата существует два варианта - если мы двигали черную клетку, стоящую в пересечении первого и второго квадратов, то движений 2, если нет - то три. Итак, можно построить дерево (см. рис.). При переходе по стрелке мы умножаем числа, стоящие в вершинах. В конце концов, числа до которых нельзя добраться, складываем. Итог - кол-во способов. Докажем по индукции, что искомое количество равно , где n - номер уровня (ступени).
База очевидна: при n=1 результат 3, что верно.
Переход: пусть для некоторого n=k верно. Докажем, что верно и для n=k+1. Рассмотрим k+1-ый уровень. Количество троек равно количеству двоек. Поэтому каждое слагаемое, входящее в сумму, которая равна можно умножить сначала на тройки, а потом на двойки, что равнозначно
, переход доказан.
Не забудем итоговый ответ также домножить на два, так как существует две различные шахматные расцветки прямоугольника.
Имеем квадратов, а, стало быть, уровней.
;
Ответ: