Предмет: Алгебра,
автор: zvezdapezda10
Помогите решить систему уравнений
Приложения:
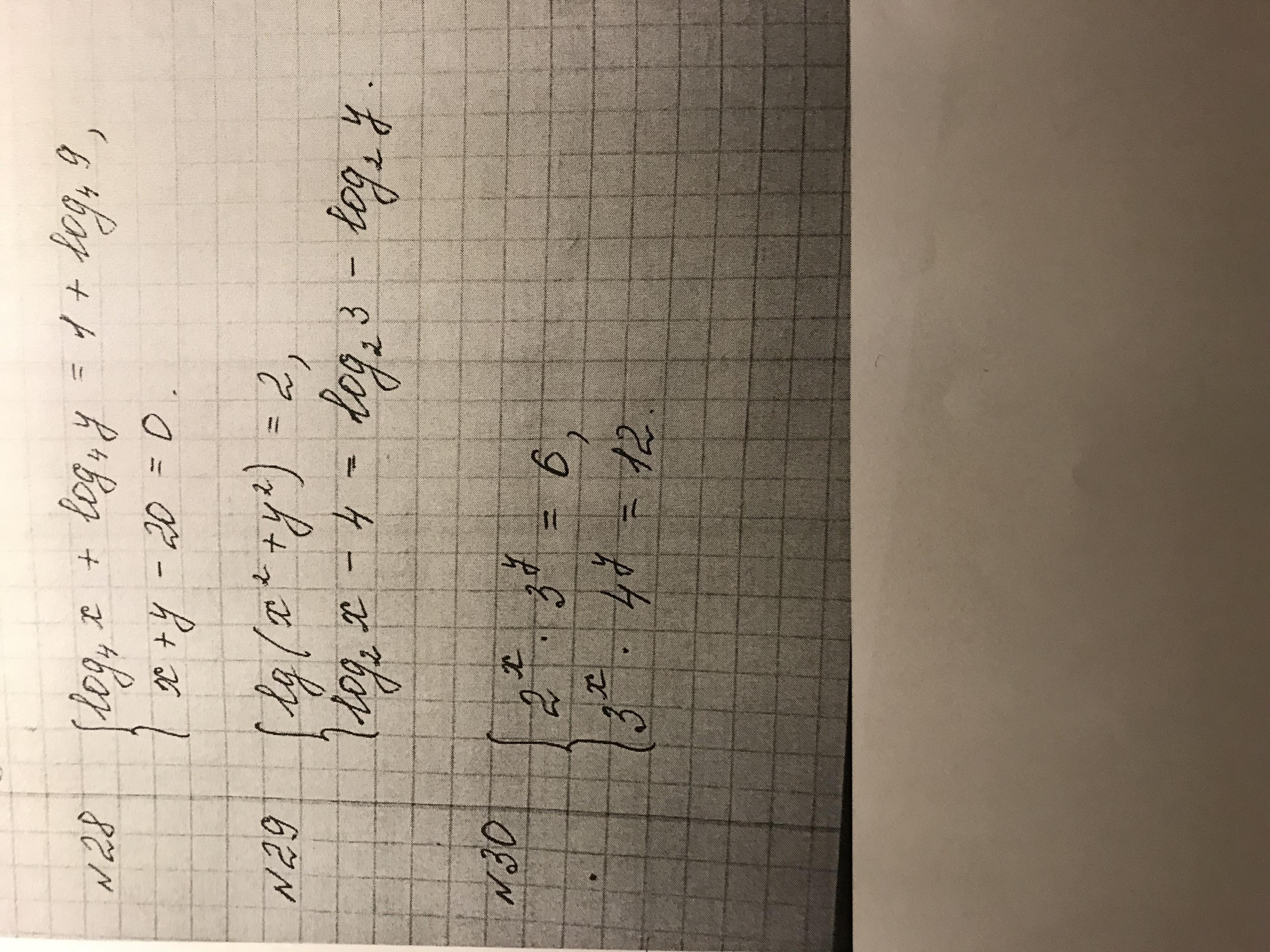
Ответы
Автор ответа:
2
Ответ:
Ответ:
Ответ:
Похожие вопросы
Предмет: Математика,
автор: trtrtrtrtt6rfty
Предмет: Биология,
автор: evelinaciksa
Предмет: Математика,
автор: dospwpqp
Предмет: Математика,
автор: лидия42