Предмет: Математика,
автор: lissette
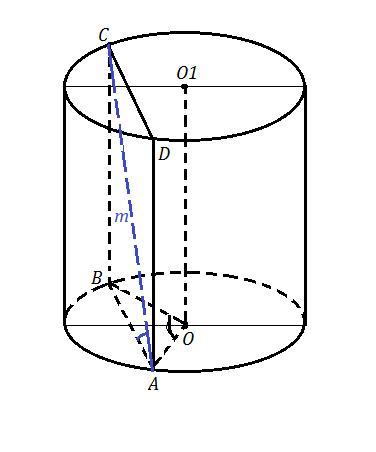
Параллельно оси цилиндра проведена плоскость, пересекающая нижнюю основу по хорде, которую видно из центра этой основы под углом 2α. Найдите площадь боковой поверхности и объем цилиндра, если диагональ полученного сечения равна m и падает на плоскость основания цилиндра под углом β.
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
∠AOB=2α , ∠BAC=β , AC=m
ΔABC: ∠ABC=90° , sin∠BAC=BC/AC ⇒ BC=AC*sin∠BAC=m*sinβ=H - высота цилиндра
сos∠BAC=AB/AC ⇒ AB=AC*cos∠BAC=m*cosβ
ΔAOB: OA=OB=R , по теореме синусов АВ/sin∠AOB=2R ⇒ R=AB/(2sin2α)=(m*cosβ)/(2sin2α)
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: yanakytikova
Предмет: Химия,
автор: Illya6577
Предмет: Биология,
автор: dimitrobossanova
Предмет: Обществознание,
автор: Милада2006
Предмет: Математика,
автор: кас10