Question

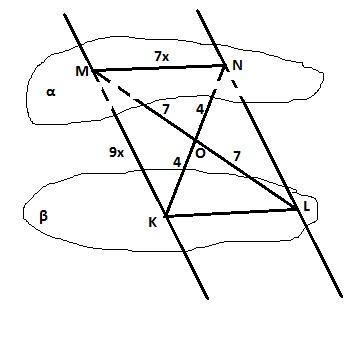
Даны параллельные плоскости α и β. Через точки M и N плоскости α проведены параллельные прямые, которые пересекают плоскость β в точках K и L. Вычислите периметр четырехугольника MNLK, если ML=14, NK=8 и MK:MN=9:7

Answer 1

Ответ:

Р = 32 ед.

Объяснение:

Через две параллельных прямых можно провести ЕДИНСТВЕННУЮ плоскость. Две параллельных плоскости пересекаются третьей по параллельным прямым. Следовательно, четырехугольник MNLK - параллелограмм. В параллелограмме диагонали, пересекаясь, делятся точкой пересечения пополам.

Рассмотрим треугольник KMN. В нем МО - медиана (О - точка пересечения диагоналей). Стороны треугольника

МК = а = 9х, MN = b = 7x, NK = c = 8. Медиана МО = m = 7 (половина диагонали ML). Тогда по формуле для медианы треугольника:

m² = (2a²+2b²-c)/4  или

196 = 162х²+98х² - 64.  =>  260х² = 260  =>  x = 1.

Значит КМ = NL = 9*1 = 9,  MN = KL = 7*1 = 7.

Периметр параллелограмма Рkmnl = 2*(9+7) = 32 ед.