к графику функции y=x+2/x-2 провести касательную так, чтобы она была параллельна прямой y=-x+2
Пожалуйста, помогите)
Ответы
Ответ:
y = -x-6
Пошаговое объяснение:
Касательная является параллельной другой прямой, если углы их наклона совпадают.
Если Вам известно понятие производной функции в точке, то можно использовать её геометрический смысл: производная в точке равна тангенсу угла наклона касательной в данной точке.
Так, например, наклон функции y=-x+2 одинаков во всех точках и равен -1, т.е. y' = -1.
Необходимо найти такие точки, принадлежащие y=x+2/x-2, в которых производная этой функции была бы равна -1.
Найдём производную: y' = 1 - 2/x^2.
Приравняем производную к -1: 1 - 2/x^2 = -1;
Отсюда следует, что x = ±1 -- это абсциссы точек, в которых производная функции равна -1.
Значения y для этих точек 1 и -5, т.е. точки (1, 1) и (-1, -5).
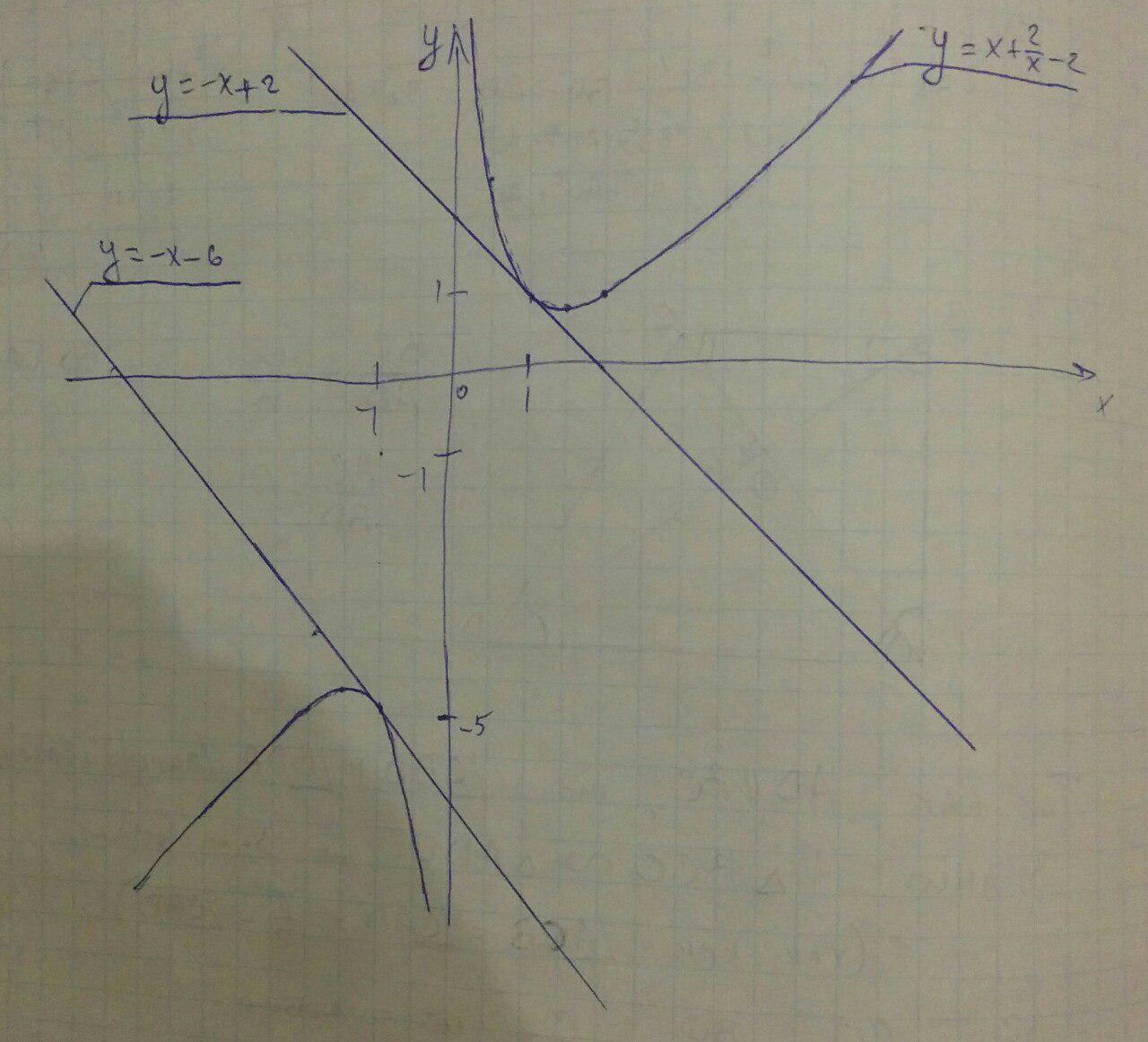
Касательной к графику функции y = x+2/x-2 в точке (1, 1) является прямая y = -x + 2, которая задана в условии. В точке (-1, -5) касательной является прямая y = -x - 6.
Если Вам неизвестно понятие производной, то просто постройте график данных функций и найдите экспериментально линейкой ту точку, в которой касательная будет параллельна y = -x + 2.
Построение в приложении.