Question

В прямоугольном треугольнике с гипотенузой AB = 21 медиана AD пересекает биссектрису BK в точке O, расстояние от точки O до катета AC равно 3 . Найдите катеты и расстояние от точки O до гипотенузы AB.

Answer 1

Ответ:

Объяснение:  Решение : /////////////////////////

Answer 2

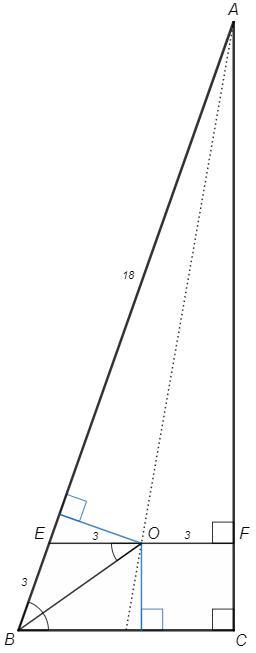
Через точку O проведем EF||BC.

В трапеции пересечение продолжений боковых сторон и середины оснований лежат на одной прямой. О - середина EF.

EO=OF=3, EF=6

Биссектриса внутреннего угла при параллельных отсекает равнобедренный треугольник (∠EOB=∠CBO, накрест лежащие. ∠EOB=∠EBO).

BE=EO=3, AE=18

△ABC~△AEF (по соответственным углам при BC||EF)

BC/EF=AB/AE =21/18 =7/6, BC=7

AC=√(21^2 -7^2) =√(14*28) =14√2

Точка О лежит на биссектрисе угла ABC, следовательно равноудалена от сторон угла. Расстояние между параллельными постоянно, поэтому достаточно найти FC.

AF/AC =6/7 => FC=AC-AF =AC/7 =2√2