Question

Нужны все задания, кто что сможет

Answer 1

$B6)\; \; log_{a^{k}}x=\frac{1}{k}\cdot log_ax\; \; ,\; \; x>0\; ,\; a>0\; ,\; a\ne 1\\\\log_{\sqrt6}\frac{36}{\sqrt7+\sqrt3}+log_{1/6}\frac{1}{10+2\sqrt{21}}=2log_6\frac{36}{\sqrt7+\sqrt3}-log_6\frac{1}{10+2\sqrt{21}}=\\\\=log_6\Big (\frac{36}{\sqrt7+\sqrt3}\Big )^2-log_6\frac{1}{10+2\sqrt{21}}=log_6\Big (\frac{36^2}{(\sqrt7+\sqrt3)^2}:\frac{1}{10+2\sqrt{21}}\Big )=\\\\=log_6\frac{6^4\cdot (10+2\sqrt{21})}{10+2\sqrt{21}}=log_66^4=4$

$B9)\; \; b_1=3\; ,\; \; b_3+b_5=60\; \; ,\; \; q<0\; (znakocheredyushijsya\; pyad)\\\\b_3+b_5=b_1q^2+b_1q^4=3q^2+3q^4=60\\\\q^4+q^2=20\; \; ,\; \; q^4+q^2-20=0\; ,\\\\q^2=-5\; \; \; ili\; \; \; q^2=4\\\\q^2=-5\; \; \to \; \; q\in \varnothing \\\\q^2=4\; \; \to \; \; q=\pm 2\\\\q<0\; \; \to \; \; q=-2\; \; ,\; \; b_2=b_1q=3\cdot (-2)=-6\\\\Otvet:\; \; b_2=-6\; .$

P.S.  Геом. прогрессия будет такая:  3 , -6 , 12 , -24 , 48 , ...

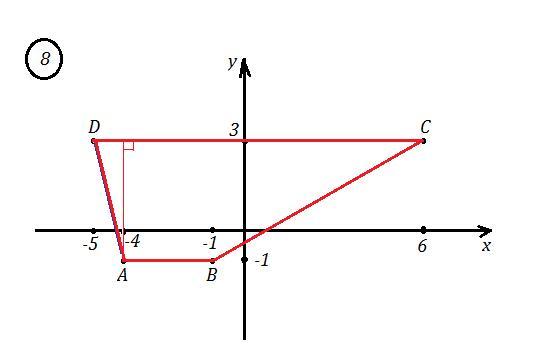
B8)   Так как точки А(-4-1) и В(-1,-1) имеют одинаковые ординаты, равные  у= -1, то эти точки лежат на одной прямой, уравнение которой  у= -1. Аналогично, точки С(6,3) и D(-5,3) лежат на прямой  у=3 . Причём, прямые  у= -1  и у=3  параллельны. Поэтому  заданная фигура - трапеция.

Длина оснований трапеции:  АВ=-1-(-4)=-1+4=3 ,  CD=6-(-5)=6+5=11 .

Высота трапеции -  это расстояние между прямыми  у= -1 и у=3 . Оно равно h=3-(-1)=3+1=4 .

Площадь трапеции равна S=((3+11)/2)*4=(14/2)*4=7*4=28 .

Cм. рисунок.