Предмет: Алгебра,
автор: 89036596178w
Не могу решить, пожалуйста помогите! Заранее спасибо!
Приложения:
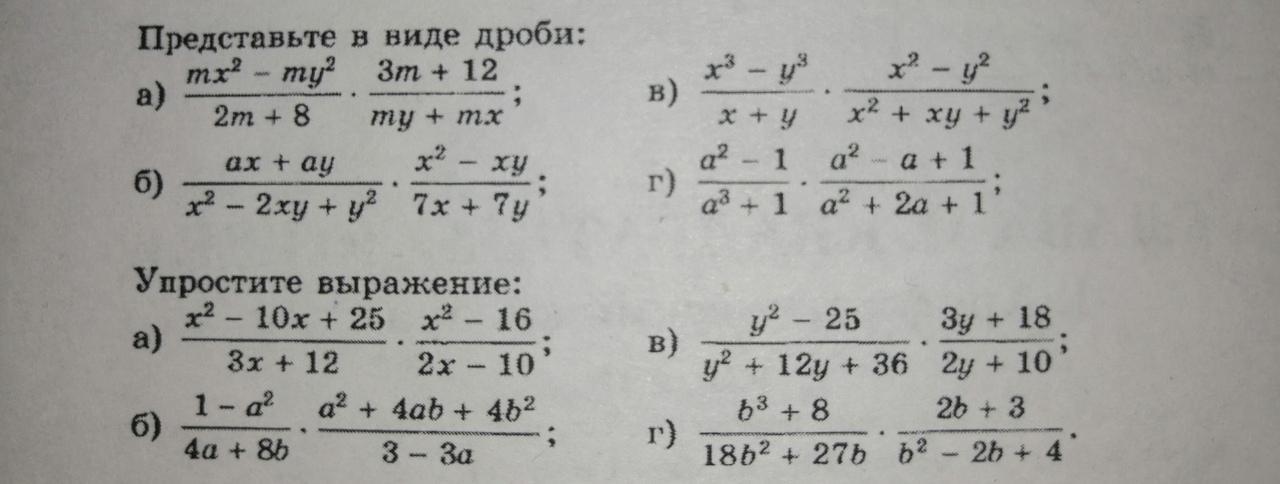
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Українська мова,
автор: stasklokov82
Предмет: Алгебра,
автор: pejmej72
Предмет: Английский язык,
автор: ademabisenova650
Предмет: Математика,
автор: Ниизвестная
Предмет: Физика,
автор: alinamalt