Предмет: Алгебра,
автор: Роман1233212002
50б. Решите уравнение. ( у меня вышло |х²-3х|=-2 ) Срочно!
Приложения:
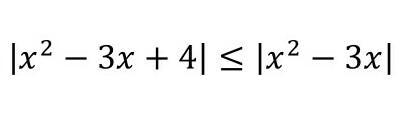
Ответы
Автор ответа:
2
Ответ:
Объяснение:
Метод рационализации - это первое, что пришло в голову, к сожалению.
| f(x) | ∨ | g(x) | ⇔ (f(x) - g(x))(f(x) + g(x)) ∨ 0
В данном случае, f(x) = x² - 3x + 4, а g(x) = x² - 3x. Подставим, решим:
(x² - 3x + 4 - x² + 3x)(x² - 3x + 4 + x² - 3x) ≤ 0
4(2x² - 6x + 4) ≤ 0 | : 8
x^2 - 3x + 2 ≤ 0
(x - 1)(x - 2) ≤ 0
Далее применим метод интервалов, получим:
+++++++++++++++++++[1]-------[2]++++++++++++>x
Значит, x ∈ [1;2]
Ответ: x ∈ [1;2]
Роман1233212002:
Классный метод, один раз с минусом перенести, другой с плюсом?
Очень быстро и удобно
Формула разности квадратов.
Существует множество вариаций этого метода для различных ситуаций, однако в школе, я думаю, их лучше не применять, ибо необоснованно.
Это верно лишь в том случае , когда обе части неотрицательны.
С другой стороны, если ты поймешь, как это выводится, то сможешь доказать работоспособность этих методов своему преподу
Тогда, я думаю, претензий от преподов не будет.
Спасибо, я абитуриент.
В вузе точно проблем не будет) Я сам не из России, но, говорят, что на ЕГЭ такие способы разрешены. Странно, что ты о них не знаешь.
И я не с России)
Автор ответа:
2
Ответ:
Х принадлежит [1;2]
Объяснение:
Откуда
Х принадлежит [1;2]
Похожие вопросы