Предмет: Алгебра,
автор: nikolenkoregina
Помогите с тригонометрией, пожалуйста!
Приложения:
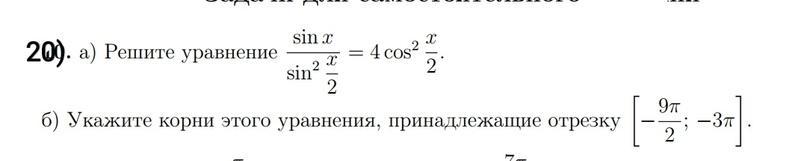
Ответы
Автор ответа:
1
Ответ:
Объяснение: sin x=4cos²x/2·sin²x/2, sinx/2≠0,x≠2πn,n∈z
sinx=sin²x ,
sin²x-sinx=0
sinx(sinx-1)=0 т.к. (2sinx/2·cosx/2=sinx)
sinx=0 или sinx=1
x=πn,n∈z x=π/2+2πn,n∈z
т.к.х≠2πn,то х=π+2πк,к∈z и х=π/2+2πn,n∈z
-3π,-3,5π∈[-4,5π;-3π] при к=-2 и n=-2
Автор ответа:
1
Похожие вопросы
Предмет: Математика,
автор: korolsasela2
Предмет: Геометрия,
автор: dimaaaaaaaaamm
Предмет: Английский язык,
автор: alexminaev
Предмет: Алгебра,
автор: Аноним
Предмет: Литература,
автор: 927024484