Предмет: Математика,
автор: ignat160
Помогите решить систему уравнений. 
Приложения:
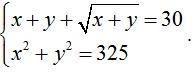
mathgenius:
sqrt(x+y)=t , дальше пошло поехало.
Ответы
Автор ответа:
2
Ответ:
(10; 15), (15, 10).
Пошаговое объяснение:
Автор ответа:
2
Ответ: y1=15 ; x1=10
y2=10 ; x2=15
Пошаговое объяснение:
Сделаем очевидную замену :
√(x+y)=t>=0
Тогда первое уравнение системы становится квадратным.
t^2+t-30=0
По Виету в уме корни:
t1=5
t2=-6 (не подходит)
√(x+y)=5
x+y=25 → x=25-y
Дальше можно решать как душе угодно ,но я предлагаю такой прием.
Возведем последнее равенство в квадрат и умножим на -1 , а второе уравнение в системе умножим на 2 :
1) -(x+y)^2=-x^2-2xy-y^2=-625
2) 2*(x^2+y^2)=650
Cложим 1 и 2 :
x^2-2xy+y^2=25
(x-y)^2=25
x-y=+-5
25-2y=+-5
y= (25+-5)/2
y1=15 ; x1=10
y2=10 ; x2=15
Класс))
Похожие вопросы
Предмет: Литература,
автор: aselyasako9451
Предмет: Українська література,
автор: KarimIlyasov6071
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: знакомьтесь