Question

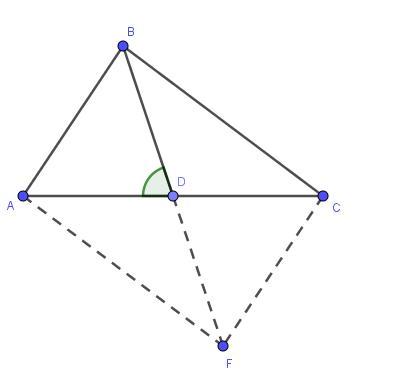
В треугольнике медиана проведенная к стороне образует угол 60 градусов. Две другие стороны равны 14 и 2√97. Найдите медиану.

Answer 1

Рассмотрим треугольник ABD. По теореме косинусов

$AB^2=BD^2+AD^2-2BD\cdot AD\cdot \cos60^\circ\\ 14^2=BD^2+AD^2-2BD\cdot AD\cdot \dfrac{1}{2}\\ \\ BD^2+AD^2-BD\cdot AD=196$

Для треугольника BDC (∠BDC = 180°-60° = 120°),  по теореме косинусов:

$BC^2=BD^2+CD^2-2BD\cdot CD\cdot \cos120^\circ\\ BC^2=BD^2+CD^2-2BD\cdot CD\cdot (-\frac{1}{2})\\ (2\sqrt{97})^2=BD^2+CD^2+BD\cdot CD$

Поскольку BD - медиана, то AD = CD. Решим систему

$\displaystyle \left \{ {{BD^2+AD^2-BD\cdot AD=196} \atop {BD^2+AD^2+BD\cdot AD=388}} \right.$

Получится $BD=16$ и $AD=6$ или $BD=6$ и $AD=16$