Помогите решить пожалуйста
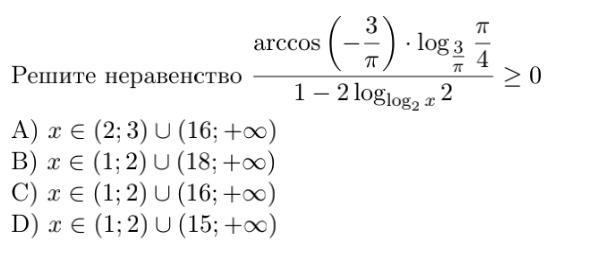
Ответы
Ответ:
(1; 2) ∪ (16; +∞).
Объяснение:
Проанализируем неравенство. Числитель представляет собой некоторую константу. Попробуем прикинуть, какой знак имеет выражение в числителе.
1. Логарифм по основанию чуть меньше единицы, значит функция будет убывающей. И если идти в "обратную" сторону, то при уменьшении аргумента от 1 до 0 значение логарифма будет большим. Поскольку п/4 < 1, то значение логарифма будет сто процентно положительным.
2. Воспользуемся свойством арккосинуса: . Значит
. Стоит отметить также, что значение арккосинуса варьируется от 0 до П. Это значит, что арккосинус тоже положительное значение.
3. Раз числитель положительный, а условие требует положительного значения выражения, значит знаменатель по знаку должен совпадать с числителем. Иными словами, все сводится к неравенству
Нетрудно догадаться, что неравенство должно быть строгим, так как знаменатель, равному нулю, никого не порадует.
Для удобства восприятия сделаем замену
Тогда неравенство будет выглядеть следующим образом:
С другой стороны, на t накладываются следующие ограничения:
Теперь все сводится к решению системы неравенств:
Решаем первое неравенство
В этом моменте кроется один ньюанс: t может принадлежать промежутку от 0 до 1, тогда в этом случае запишется неравенство как , т.е. решением является t, принадлежащей промежутку (0; 1). Но t также может быть больше 1, в этом случае неравенство запишется как
Значит, справедлива система
Заменив везде t на , и выразив x. получаем:
Этому соответствует промежуток (1; 2) ∪ (16; +∞). то есть ответ C