Геометрия.
Дано:
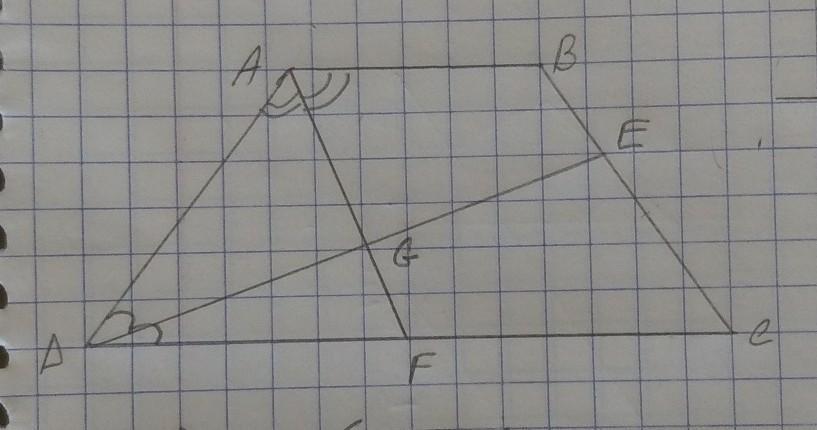
ABCD трапеция
Угол ADE = EDC
Угол DAF = BAF
Доказать:
А) AF _|_ DB
B) AG = GF
Спс.
Ответы
Ответ:
Объяснение: !!! ВОЗМОЖНО У ВАС ОШИБКА И НАДО ДОКАЗАТЬ ПЕРПЕНДИКУЛЯРНОСТЬ AF И DE, А НЕ DB.
Т.К. АВ || CD И AF - СЕКУЩАЯ, ТО∠АFD = ∠BAF, ПОЛУЧИЛИ ЧТО В ТРЕУГОЛЬНИКАХ AGD И FGD ДВА УГЛА РАВНЫ МЕЖДУ СОБОЙ, ЗНАЧИТ И ТРЕТЬИ УГЛЫ ТОЖЕ РАВНЫ, Т.Е. ∠AGD =∠FGD. ∠AGE = ∠FGD Т.К. ОН ВЕРТИКАЛЬНЫЕ. ПОЛУЧИЛИ ∠AGD =∠FGD = ∠AGE. ЗНАЧИТ ∠EGF РАВЕН КАЖДОМУ ИЗ ТРЕХ. Т.О ВСЕ ЧЕТЫРЕ УГЛА РАВНЫ. ЗНАЧИТ 360° : 4 = 90°. СЛЕДОВАТЕЛЬНО AF ⊥ DE.
Δ AGD = Δ FGD ПО ОБЩЕЙ СТОРОНЕ GD И РАВНЫХ УГЛАХ ADG И GDF, AGD И FGD ПОЛУЧИМ, ЧТО AG = GF.
Объяснение:
А)Неверно, можно доказать, что DE перпендикулярно AF. Это следует из того, что 180(т. к. дана трапеция)=BAD+ADF=(BAF+FAD)+(ADE+EDC)=2FAD+2ADE, откуда FAD+ADE=180/2=90.
AGD=180-(FAD+ADE)=180-90=90
Б)BAF=AFD(как накрест лежащие при параллельных прямых AB и DC)
DGF=180-AGD(смежные углы)=180-90=90
треугольники AGD и FGD равны(по общей стороне DG и прилежащим к ней углам)
Из равенства треугольников AGF и FGD следует равенство сторон AG и GF, ч.т.д.