мне нужно знать как решать, последовательность , обьясните суть как это надо делать, не просто написать решение, а вообще как это делать и с чего начинать? Например, надо вот это взять и отнять от этого , потому что. Подробно , я ничего не знаю по этой теме, как ее понять? Подробно
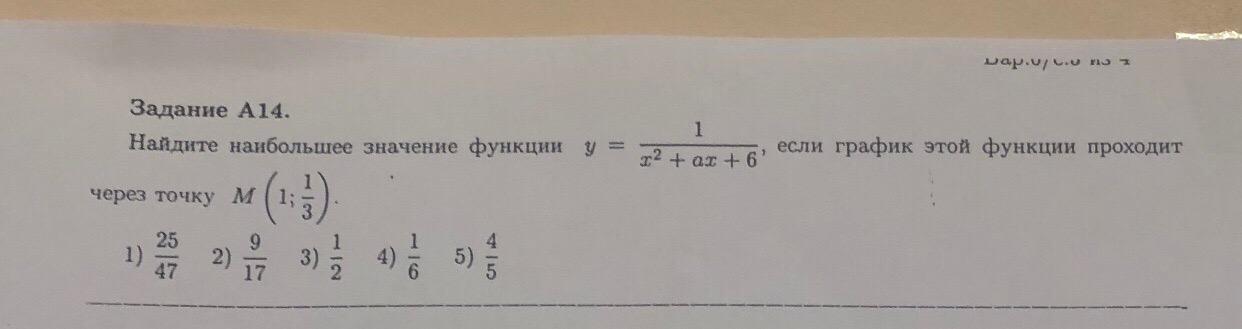
Ответы
Ответ под номером 3) 1/2

Ответ:
3) 1/2.
Пошаговое объяснение:
Рассмотрим функцию у = 1/(х^2+ах+6).
1. График функции проходит через точку М(1;1/3), подставим её координаты в формулу:
х =1, у = 1/3, тогда
1/3 = 1/(1^2+а•1+6)
1/3 = 1/(7+а)
7+а = 3
а=7-3
а=4,
формула примет вид
у = 1/(х^2+4х+6).
2. Правая часть равенства - дробь, числитель которой не меняется, именно поэтому значение дроби будет наибольшим, когда знаменатель является наименьшим. (Например, 7>3, но 1/7 < 1/3).
Найдём наименьшее значение квадратного трёхчлена х^2+4х+6. Сделать это можно двумя способами.
1 способ:
Рассмотрим функцию g(x) = х^2+4х+6. Её графиком является парабола, ветви которой направлены вверх, т.к. а=1, 1>0. Такая функция достигает своего наименьшего значения в вершине параболы.
х вершины = -b/(2a) = - 4/2 = -2.
y вершины = (-2)^2+4•(-2)+6 = 4-8+6=2.
2 - наименьшее значение функции g(x), наименьшее значение квадратного трёхчлена.
2 способ:
х^2+4х+6 = х^2+4х+4+2 = (х+2)^2 +2.
(х+2)^2 неотрицательно при любых значениях х, т.е. наименьшее значение этого слагаемого равно нулю. Тогда наименьшее значение суммы (х+2)^2 +2 равно 0+2=2. 2 - наименьшее значение квадратного трёхчлена.
3. Итак, в дроби 1/(х^2+4х+6). наименьшее значение знаменателя равно 2, тогда наибольшее значение самой дроби равно 1/2.
Наибольшее значение функции у = 1/(х^2+4х+6) равно 1/2.