Предмет: Геометрия,
автор: pand53
ПОМОГИТЕ СРОЧНО!!
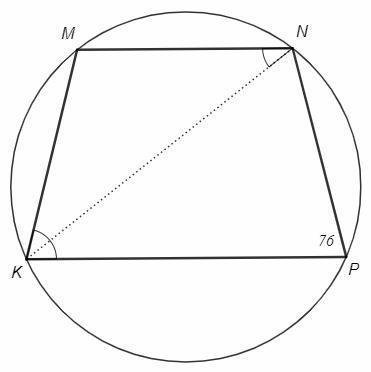
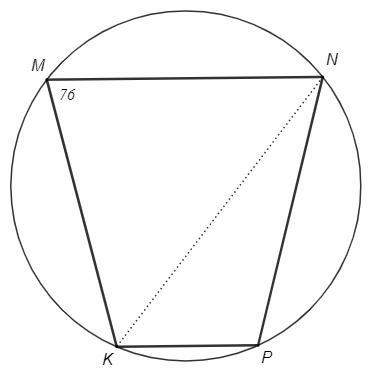
Вершины трапеции KMNP (MN || KP) лежат на окружности. Диагональ KN – биссектриса угла МКР. Один из углов трапеции 76˚ͦ. Найдите дуги, на которые вершины трапеции разделили окружность.
Ответы
Автор ответа:
1
MNK=PKN (накрест лежащие при MN||KP)
MKN=PKN (KN – биссектриса MKP)
Равные вписанные углы опираются на равные дуги.
∪KM=∪MN=∪NP=x
∪KP=y
1) KPN=76
KPN =(∪KM+∪MN)/2 =x =76
3x+y =360 => y=360-76*3 =132
2) KMN=76
KMN =(∪KP+∪NP)/2 =(x+y)/2 =76 => x+y=152
3x+y =360 => x=(360-152)/2 =104
y=152-104=48
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: kirillrogacko
Предмет: Алгебра,
автор: dipsikmal
Предмет: Алгебра,
автор: Аноним
Предмет: Математика,
автор: Linik2005