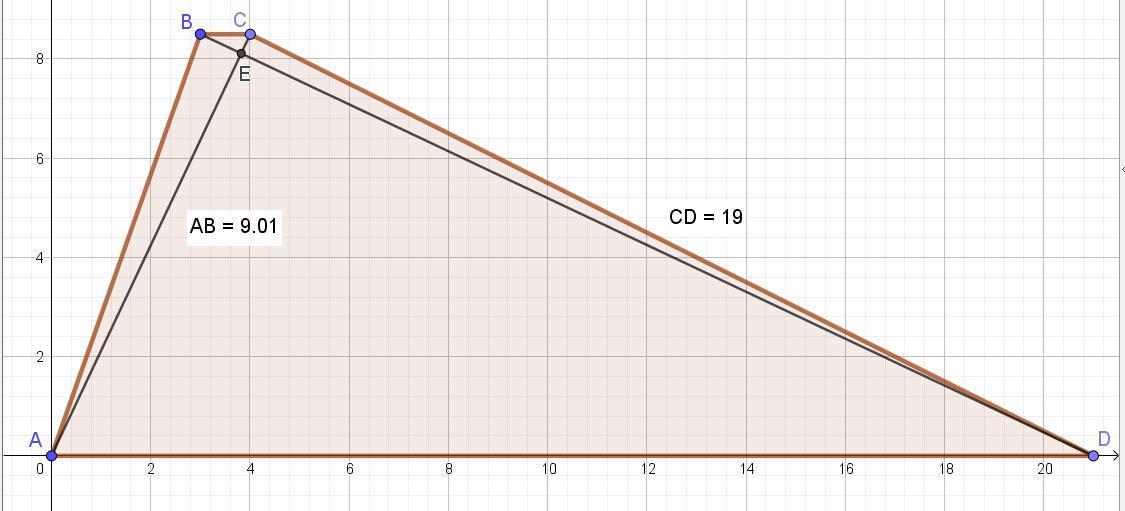
найдите углы трапеции при её большей боковой стороне если известно что диагонали трапеции взаимно перпендикулярны её основании равны 1 и 21 а одна боковая сторона равна 19
Ответы
Чтобы диагонали пересекались под прямым углом именно сторона 19 должна быть большей из боковых сторон заданной трапеции.
Пусть точка пересечения диагоналей - точка Е.
Треугольники ВЕС и АЕД подобны с коэффициентом 1:21.
Обозначим отрезки диагоналей:
СЕ = х, АЕ = 21х.
ВЕ = у, ДЕ = 21у.
В треугольнике ВЕС соотношение: х² + у² = 1. Отсюда у² = 1 - х².
Рассмотрим треугольник СЕД.
х² +(21у)² = 19². Заменим у² = 1 - х².
х² + 441 - 441х² = 361,
440х² = 80,
х = √80/440) = √(2/11).
у = √(1 - (2/11)) = √(9/11) = 3/√11 = 3√11/11.
Теперь можно определить углы при стороне СД, равной 19 ед.
∠(АДЕ) = arc tg(21x/21y) = arc tg(x/y) = arc tg(√(2/11)/(3√11/11) = arc tg(√2/3) =
= 0,44051 радиан = 25,2394 градуса.
∠(CДЕ) = arc sin(x/19) = arc sin(√(2/11)/(19) = arc sin(√2/209) =
= 0,04757 радиан = 2,7256 градуса.
Ответ: угол СДА равен 25,2394 + 2,7256 = 27,9650 градуса.
угол ВСД равен 180 - 27,9650 = 152,035 градуса.