Предмет: Математика,
автор: kirillart5
предел по определению : постоянное число a называется пределом переменной величины x , если для каждого заданного положительного произвольно маленького числа ε можно указать такое значение переменной x, что все последующие значения переменной будут удовлетворять неравенству | x - a | < ε .
Теперь к сути - в учебниках приводятся примеры с положительными пределами типа a = 1, при x = 1/n или др. Тут все ясно - в окрестностях единицы можно взять значение которое будет удовлетворять данному условию.
Но меня мучает вопрос - а что если предел будет отрицательным? например -1 или -2, не важно. Какое значение будет принимать ε, ведь сказано что оно положительное и как все это дело будет удовлетворять неравенству | x - a | < ε
MizoriesKun:
Если а = -1 ; |х- (-1)|= | х+1| ;
а за что тогда принимать ε? эта величина будет отрицательной или положительной ?
е всегда положительна ( это радиус окрестности ) , минус остается внутри модуля
короче , е - это любое положительное число и оно не зависит от знака предела , по этому числу подбирают дэльту , если считают предел функции или номер N , если предел последовательности
сейчас для предела последовательности напишу
понятно, пасиб
Ответы
Автор ответа:
2
Ответ:
Пошаговое объяснение:
Определение и решение конкретного примера , при условии , что
a < 0 и b < 0 :
Приложения:
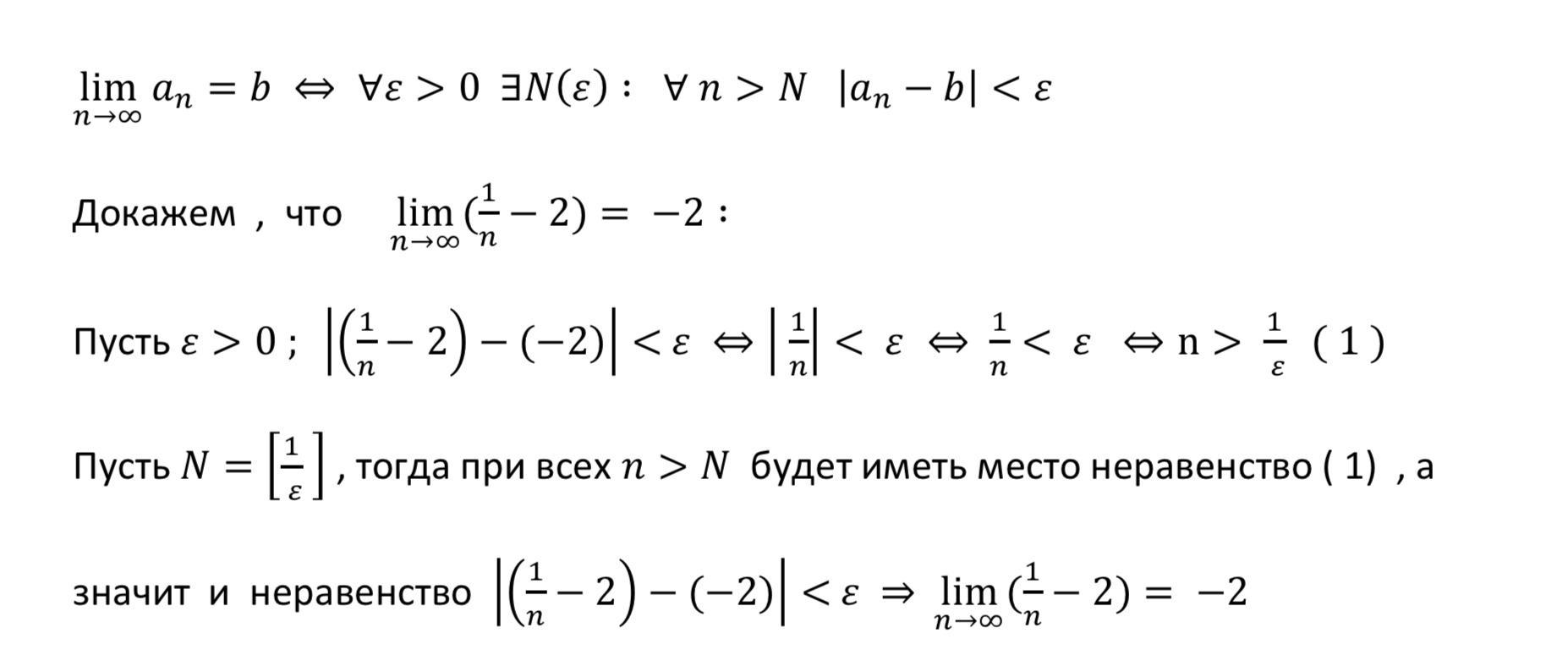
хм, а всегда N должно равняться e?
в примере N равно не е , а целой части 1/e , это разные вещи , если N будет равна целой части 1/e , то для всех n больших N будет выполняться неравенство | a(n) -b| < e , то есть утверждение доказано
Похожие вопросы
Предмет: Математика,
автор: cjfjfc
Предмет: Физика,
автор: inna22063
Предмет: Математика,
автор: vnoi228
Предмет: Математика,
автор: vika453637
Предмет: История,
автор: кунгфульвёнок4