Question

отрезок ВМ медиана треугольника АВС. На продолжении отрезка МВ точки В обозначили точку D так, что BD=BC. Известно, что AD=2BM, угол CBM=40 градусов. Найдите угол ADB
ОЧЕНЬ ПРОШУ ПОМОГИТЕ​

Answer 1

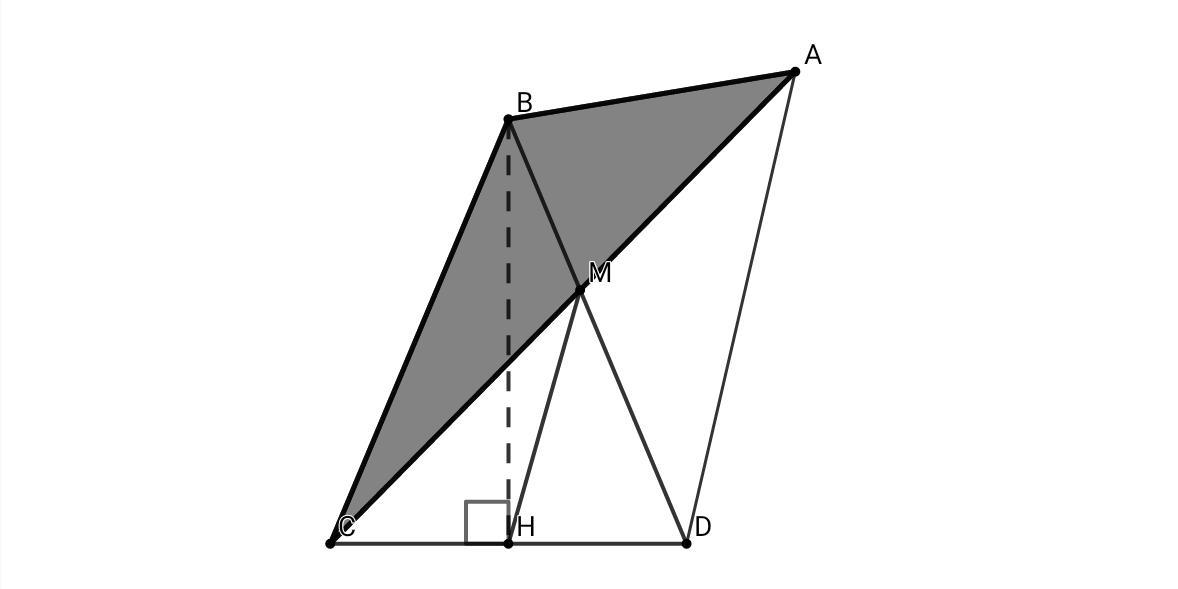
В ΔВСD, BD = BC, опустим высоту ВН на CD ⇒ CH = HD , ∠DBH = ∠CBH = 20° , ∠BDC = ∠BCD = 70°

CH = HD, AM = CM ⇒ MH - средняя линия ΔАСD, MH || AD , MH = AD/2 = BM , MH = BM ⇒ ΔBMH = равнобедренный, ∠МВН = ∠МНВ = 20° , ∠МНD = 90° - 20° = 70° = ∠MDH ⇒ ΔDMH - равнобедренный ⇒ BM = MD = MH

∠HMD = ∠ADM = 40°  как накрест лежащие углы при MH || AD и секущей DM.

Также можно заметить, что диагонали четырёхугольника ABCD делятся точкой пересечения пополам ⇒ АВСD - параллелограмм

ОТВЕТ: 40°

Answer 2

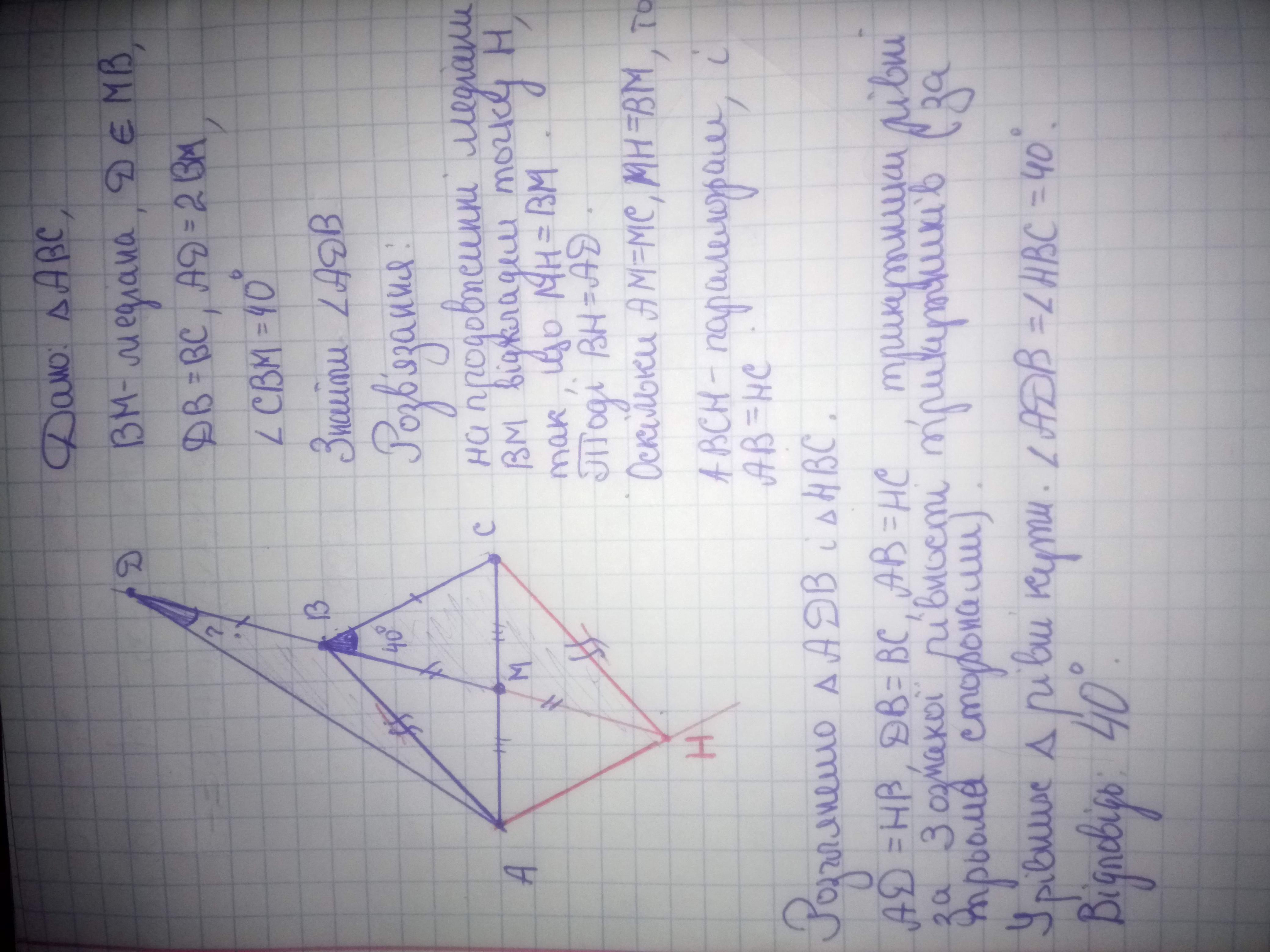
Ответ 40°. Вы в переводе на русский не указали, где точка В. В условии (оригинал написано "за В"). Поэтому мой рисунок по вашему условию.