Найдите все значения параметра а, при каждом из которых система (фото в закрепе) имеет 1 решение. Пожалуйста с объяснением. Ответ: а€ [0;1) в объединении с {-5/3;-1/3}
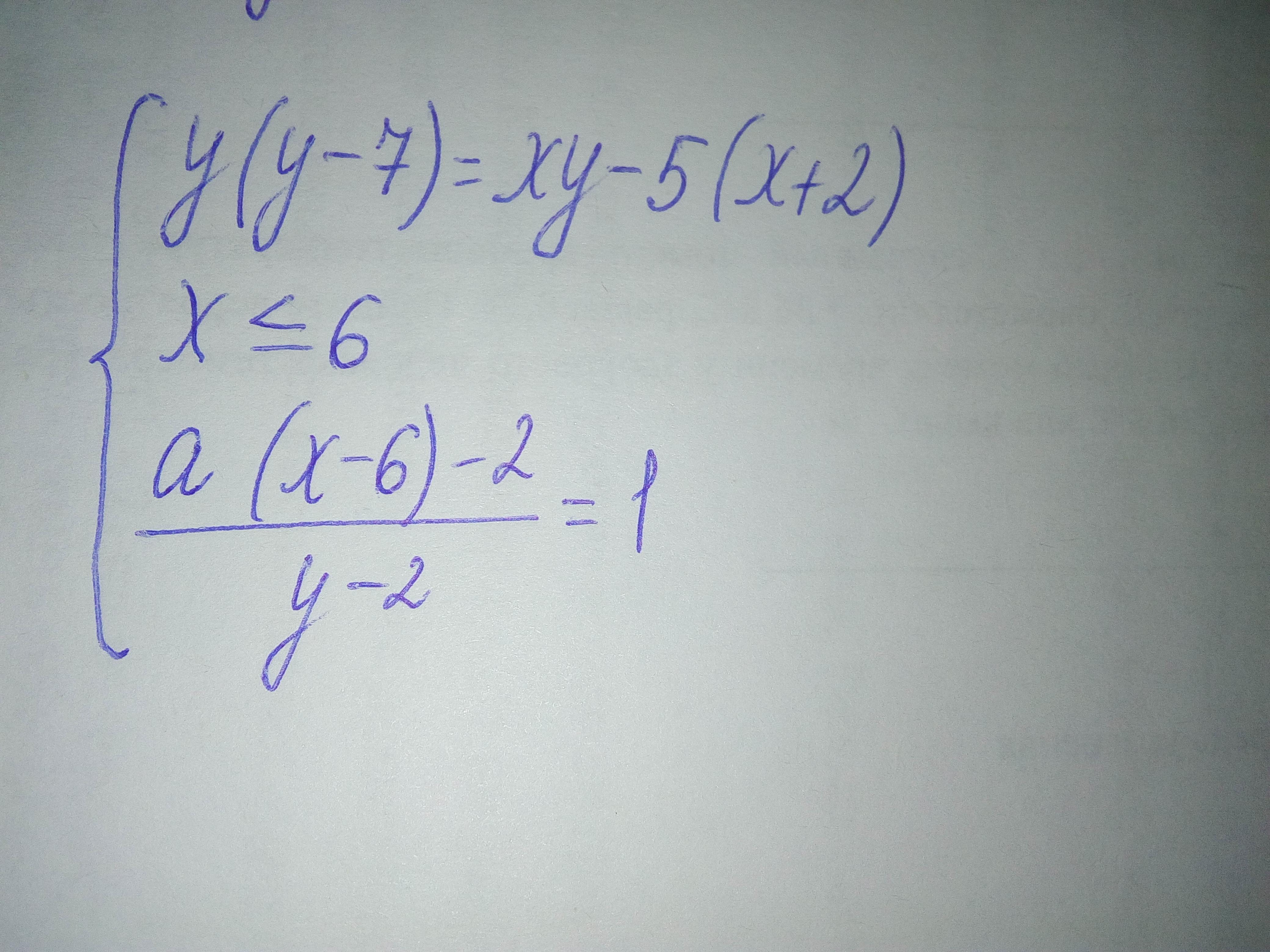
Ответы
Рассмотрим первое уравнение:
Можно построить этот график. Учитывая неравенство, строим до прямой x = 6.
Рассмотрим второе уравнение:
График этого уравнения — прямая, проходящая через точку (6; 0) с меняющимся углом наклона. Причём из него же следует, что точку с y = 2 можно выколоть на графике первого уравнения.
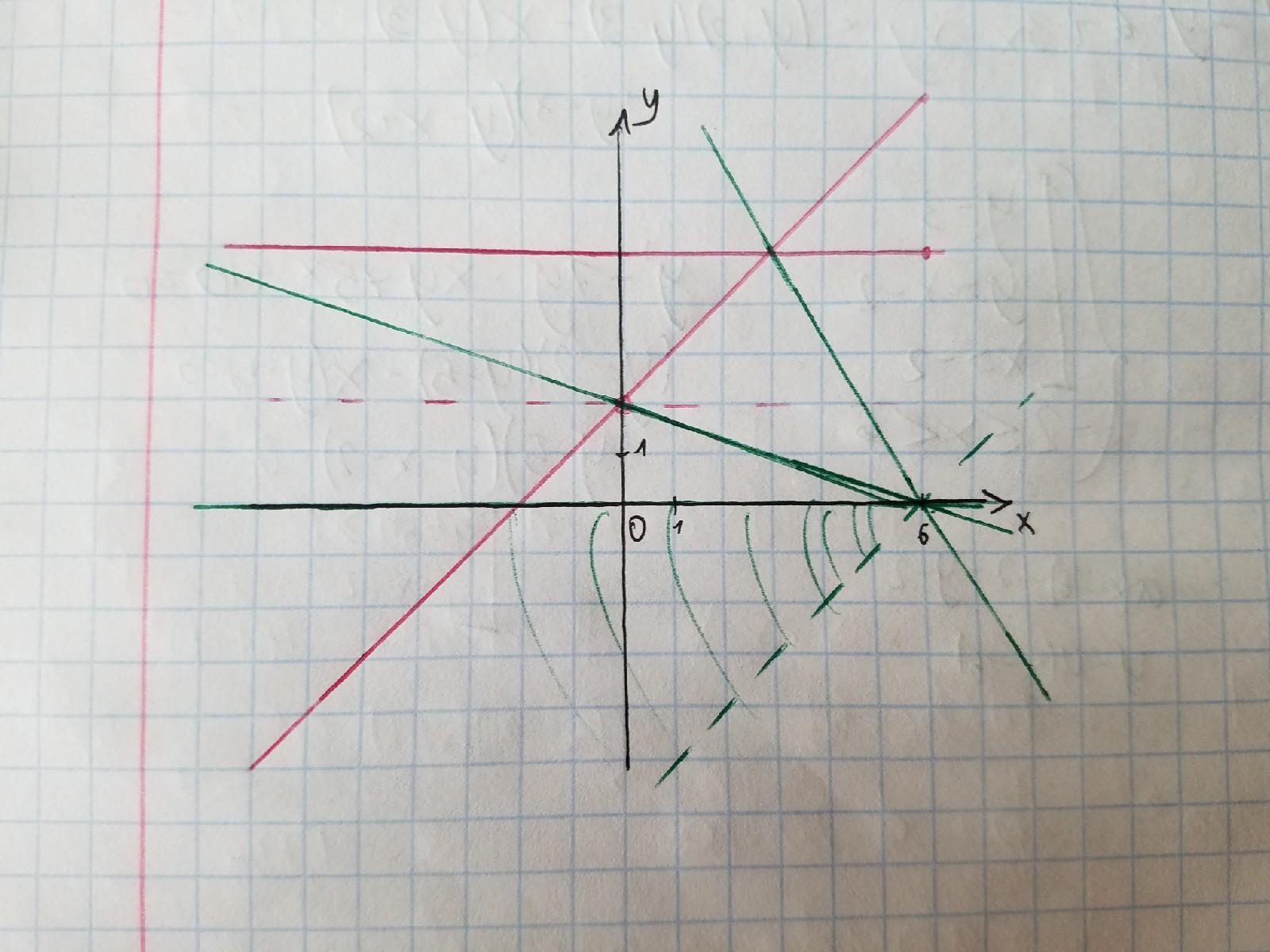
График первого уравнения начерчен красным цветом, вариации второго — зелёным.
Возьмём a = 0 и будем увеличивать угол наклона. До a = 1 будет ровно одно пересечение. При a ≥ 1 прямая либо будет параллельна прямой y = x + 2, либо не будет иметь пересечений.
Если уменьшать угол наклона, то при отрицательных a будет два решения, за исключением случаев, когда прямая проходит через выколотую точку (0; 2) и "общую" точку (3; 5):
- При (0; 2)
- При (3; 5)
Ответ:
Ответ:
Объяснение:
Решение в приложении. Должно быть понятно




